Walter Rudin 数学分析原理 9 多元函数
多元函数 functions of several variables
主要讨论 euclidean n-space $R^n$ 中
线性变换 linear transformations
9.1
- 向量空间vector space,加法封闭,scalar数乘封闭
- 线性组合linear combination,张成 生成span
- 每一个 生成 是向量空间
- 线性无关independent, $\sum c_{i}x_{i}=0$可推出 所有$c_{i}=0$ (任一个不能被其它线性表出)
- 空间X 含有由r个向量,组成无关集,不含r+1个向量的无关集,X是r维, dim X = r
- X的一个无关子集 能 span X,那么 这个子集称作一个基
- {$e_1,\dots,e_{n}$称作$\mathbb{R}^n$的标准基 standard basis
9.2 dim span{$x_1,…,x_r$} $\le r$
- 生成空间dim <= 向量个数
- S=上述向量,生成X, S是r元(不一定无关)
- Q= 个数r+1,且是无关, $y_1 \dots$
- $S_i=$ S中去掉最后i个,(这些去掉的可以由Q中表出,因此Q中要取i????个??????? )
- 没看懂 如何控制i个替换 且 保持span不变的?????????????????????????????????????????????
- 大概 S去掉i个,用Q中i个替换,那么 如果保持span X不变, Q中$_{i+1}$ 可以被线性表出,
- 必定有$S_i$中必定有 $x_{k}$ 是 $S_i$并$y_{i+1}$ 的其余元的线性组合
- 反证: 所有$x_k$都不能这样表出,那么S中系数为0, 则 Q无关会使得 无方案,( 这里 系数为0的意思是,每个$x_i$ )
- 因此 至少有个可以表出,可以表出,则剔除掉
- 推论dim $R^n=n$
- 证明 9.2 $\leq$
- 标准基 $\geq$
9.3 dim X= n情况下
- X的n个向量的集合E能生成X,当且仅当E是无关的
- E并y 是 相关
- 如果E无关 y则可被表示,所以X被生成
- 如果E相关,E可去掉一个元素不改变生成 而 dim X = n < E的向量个数 矛盾
- E并y 是 相关
- X必定有基,每个基n个向量组成
- dim的定义是最大无关集向量个数,所以 能找到n个向量无关集,上面一条说明这个无关集是基
- 任何小于r维的无关组可以扩充成基
- 小于时, 总存在一个 不可被表出的可以添加
9.4 线性变换 linear transformation
- 向量空间X 到 向量空间 Y的一个映射A
- 满足
- $A(x_1+x_2)=Ax_{1}+Ax_{2}$
- $A(cx)=cAx$
- 如果 A是线性的,时常把A(x)写作Ax
- $x=\sum c_{i}x_{i}$ 分解下的线性变换
- $Ax=\sum c_{i}Ax_{i}$
- X到X的线性变换, 一般叫做linear operators on X
- 把X映满 则A可逆,还可定义逆映射,也是线性的
9.5 A是可逆的,当且仅当 值域是$X$全体
- A基 可逆 需要线性无关,也是基,值域是全体
9.6
- $L(X,Y)$ 是X到Y 全体线性变换构成的集合
- L(X)是L(X,X)的简写
- 线性变换的集合 是线性的
- A in L(X,Y), B in L(Y,Z) 那么AB的复合 (BA) in L(X,Z)
- A in L(R^n,R^m)
- norm A: $||A|| = \sup |Ax|$, $|x| \leq 1$
- 这意味着,范数 是单位球面上所有向量经过 A 变换后长度的最大值。换句话说,范数表示了 A 将向量拉伸到多大。
- $|Ax|\le ||A|| \cdot|x|$
- norm A: $||A|| = \sup |Ax|$, $|x| \leq 1$
9.7
- A in L(R^n,R^m), 则 $||A|| < \infty$且 为 一致连续映射
- $||A+B||\leq||A||+||B||$, $||cA||=|c|\cdot ||A||$
- $||A-B||$ 作为距离,构成度量空间
- 从范数理解也可以理解,对于球面上 能拉到最大的原始,如果相同那么拉的结果 还要检查三角不等式,如果原来每个都没有同时拉最大,同样三角不等式而且三角不等式的两个值更小
- $A \in L(R^n,R^m), B \in L(R^m,R^n)$ 则 $||BA|| \leq ||B||,||A||$
- 证明:
- 按标准基展开x $|Ax|=|A \sum c_{i}x_{i}|=|\sum c_{i}Ae_{i}|\leq \sum |c_{i}||Ae_{i}| \leq \sum |Ae_{i}| < \infty$
- 一致连续 $|Ax-Ay| \leq ||A||, |x-y|$
- $|(A+B)x|=|Ax+Bx|\leq |Ax|+|Bx|\leq (||A||+||B||)|x| \leq ||A||+||B||$, $|x|\le 1$, 同时取 sup得证
- $|(BA)x|=|B(Ax)|\leq||B|||Ax|\leq||B||||A|||x|$
9.8 $\Omega$为$R^n$上所有可逆 算子的集合
- $A \in \Omega,B \in L(R^n)$ 且 $||B-A|| \cdot ||A^{-1}|| < 1$
- 则 $B \in \Omega$ emmm 可以判断可逆!?
- $\Omega$是$L(R^n)$的开子集,and the mapping $A \to A^{-1}$ is continuous on $\Omega$
- 证明
- $||A^{-1}||=\frac{1}{\alpha}$, $||B-A||=\beta$ 那么$\beta<\alpha$
- $\alpha |x|=\alpha |A^{-1}Ax| \leq a ||A^{-1}|| |Ax|=|Ax| \leq |(A-B)x|+|Bx| \leq \beta |x| + |Bx|$
- 即 $(\alpha-\beta)|x| \le |Bx|$
- 有x非0时 Bx 非0,所以 核空间只有0向量,B是可逆的,哇哦!!!
- $(\alpha-\beta)|B^{-1}y|\leq|BB^{-1}y|=|y|$
- 即$||B^{-1}|| \leq(\alpha-\beta)^{-1}$
- $||B^{-1}-A^{-1}||\leq||B^{-1}||\cdot||A-B||\cdot||A^{-1}||\leq \frac{\beta}{\alpha(\alpha-\beta)}$
- 说明 $B\to A$时$\beta\to{0}$ $B^{-1}\to A^{-1}$ 说明的反函数的映射是连续的,可以控制 可逆矩阵的距离 从而 控制其逆矩阵的距离,这里距离是上面的norm(B-A)
- 有了 可逆是开,那么当有可逆矩阵时能找到邻域内全是可逆矩阵
9.9 矩阵 matrix
- amazing !!! 现在才讲矩阵
- $x_i$,$y_{i}$分别是X,Y的基
- $A \in L(X,Y)$ 确定一组$a_{ij}$
- 满足$Ax_{j}=\sum_{i=1}^{m}a_{ij}y_{i}, 1 \leq j\leq n$, 需要注意的是A是变换,这里的$a_{ij}$会随着选择的 基不同 而不同,不只是会随着A变
- 把这些 $a_{ij}$ 写成m行n列的,叫做矩阵$[A]$
- 这里 A表示变换, $[A]$表示矩阵
- 可以说 A的值域 由 $[A]$ 的列向量生成的
- 对于X中任意向量$x=\sum c_{i}x_{i}$
- $Ax=\sum_{i=1}^{m}\left( \sum_{j=1}^{n} a_{ij}c_{j} \right)y_{i}$
- 定义 $[B][A]=[BA]$ 乘法运算,根据 变换的符合来定义 矩阵的复合
- 也就是 给定基下,B的矩阵 与 A的矩阵 的 复合 = BA复合变换 的矩阵
- 虽然上述理论可以选择基,后续处理,考虑使用$R^n$的标准基
- $|Ax|^2=\sum_{i}\left( \sum_{j}a_{ij}c_{j} \right)^2 \leq \sum_{i}\left( \sum_{j}a_{ij}^2 \cdot \sum_{j}c_{j}^2 \right)$这里又是Schwarz不等式
- $=\sum_{i,j} a_{ij}^2 |x|^2$
- 所以 $||A||\leq \sqrt{ \sum_{i,j} a_{ij}^2}$
- 如果用$B-A$代替上面的A, 说明矩阵中,某些$a_{ij}$ 是 参变量是连续函数时,A也是连续的,因为 这些参变量 连续可以控制 右侧的大小,反过来控制 $||B-A||$的大小
微分法 Differentiation
9.10 前言
- 在实数里用的 $\lim_{ h \to 0 }\frac{f(x+h)-f(x))}{h}$
- $f(x+h)-f(x)=f’(x)h+r(h)$
- 余项r(h) 很小 $\lim_{ h \to 0 } \frac{r(h)}{h}=0$
- we can therefore regard the derivative of f at x, not as a real number,but as the linear operator on $R^1$ that takes h to f’(x)h
- 注意 每个实数a 都能引出$R^1$上的线性算子,所说的这个算子,只是用a去乘,
- conversely, every linear function that carries $R^1$ to $R^1$ is multiplication by some real number.
- 正是 $R^1$与$L(R^1)$之间的这个1-1对应关系
- 其次考虑$f: R^1 \mapsto R^m$
- 导数被定义为 $\lim_{ h \to 0 } \left[ \frac{f(x+h)-f(x)}{h} -y \right]=0,y \in R^m$
- 如果y存在, $f(x+h)-f(x)=hy+r(h)$
- 其中 $h\to 0$时 $r(h)/h \to 0$
- 主项是 $h\in R^1$到$hy\in R^m$的线性变换
- $f’$ 看成$L(R^1,R^m)$的一员
- 或者说 $\lim_{ h \to 0 } \frac{f(x+h)-f(x)-f’(x)h}{h}=0$
- 等价的 $\lim_{ h \to 0 } \frac{|f(x+h)-f(x)-f’(x)h|}{|h|}=0$
- 导数被定义为 $\lim_{ h \to 0 } \left[ \frac{f(x+h)-f(x)}{h} -y \right]=0,y \in R^m$
9.11 E是$R^n$中的开集, $f$把E映入$R^m$内, $x\in E$, 如果存在$A\in L(R^n,R^m)$ 使得
- $\lim_{ h \to 0 } \frac{|f(x+h)-f(x)-Ah|}{|h|}=0$
- 那么 称f在x可微,且 记作 $f’(x)=A$
- 显然 $h\in R^n$, 开集+足够小 => x+h属于E => f(x+h)有定义, 分子绝对值内 $\in R^m$
9.12 唯一性问题,就像之前 实数中,会考虑 左导数右导数一样,而这里的h感觉上是以球面的所有点,以半径趋于0
- 唯一性 思想就是做差,
- 对于每个h $\frac{|B(th)|}{|th|}\to 0, t\to 0$
9.14 A’(x)=A
- A(x+h)-Ax=Ah
9.15 E是$R^n$的开集,f把E映入$R^m$内, f在$x_0\in E$可微,g把包含 f(E)的一个开集映入$R^k$内, g在$f(x_0)$可微, F(x)=g(f(x))
- $F’(x_0)=g’(f(x_{0}))f’(x_{0})$
- 根据定义 证明足够近
9.16 偏导数, 开集$E\subset R^n$映入$R^m$的函数f, $e_i,u_i$分别是标准基
- $f(x)=\sum_{i=1}^{m} f_{x} u_{i}, x\in E$
- $f_i(x)=f(x)\cdot u_{i}$
- $\frac{\partial}{\partial x_{j}}(f_{i})(x)=\lim_{ t \to 0 } \frac{f_{i}(x+te_{j})-f_{i}(x)}{t}$
如果已知f在某点x可微,那么,它的各个偏导数必在x处存在,并且它们能完全决定线性变换$f’(x)$
9.17 设f把开集$E \subset R^n$映入$R^m$内,f在点$x\in E$可微,那么$D_{j}f_{i}(x)$存在,且
- $f’(x)e_{j}=\sum_{i=1}^m (D_{j}f_{i})(x)u_{i}$
- 证明:
- 固定j, f在x可微
- $f(x+te_j)-f(x)=f’(x)(te_{j})+r(te_{j})$
- $\lim_{ t \to 0 } \frac{f(x+te_{j})-f(x)}{t}=f’(x)e_{j}$
- $\lim_{ t \to 0 } \sum_{i=1}^m \frac{f_{i}(x+te_{j})-f_{i}(x)}{t}u_{i}=f’(x)e_{j}$
- t趋于0时,每个商有极限4.10, 因此每个偏导存在
- 推论
- $[f’(x)]$ 是关于上述标准基的$f’(x)$的表现矩阵,那么$f’(x)e_{j}$是$[f’(x)]$ 的第j个列向量
- $h=\sum h_{j}e_{j}$
- $f’(x)h=\sum_{i=1}^{m}\left[ \sum_{j=1}^{n} (D_{j}f_{i})(x) h_{j} \right]u_{i}$
9.18 $\gamma$把$(a,b) \subset R^1$映入开集 $E \subset R^n$可微映射
- 也就是可微曲线
- f是域E上的实值可微函数
- $g(t)=f(\gamma(t))$
- $g’(t)=\sum f’(\gamma(t))\gamma’(t)$ 行矩阵乘上列矩阵 得到1x1的矩阵 也就是当个数
- $g’(t)=\sum_{i}^{n} (D_{i}f)(\gamma(t))\gamma’_{i}(t)$
- 定义 梯度nabla $(\nabla f)(x)=\sum_{i=1}^{n}(D_{i}f)(x)e_{i}$ 是一个行矩阵
- 因为$\gamma’(t)=\sum_{i=1}^{n}\gamma’{i}(t)e{i}$ 按 标准基表示
- 所以 $g’(t)=(\nabla f)(\gamma (t))\cdot \gamma’(t)$ 行矩阵 x 列矩阵
- $\gamma(t)=x+tu, |u|=1$, x,u都是向量
- $\gamma’(t)=u$
- $g’(0)=(\nabla f)(x+0u)\cdot u$
- $g(t)-g(0)=f(\gamma(t))-f(\gamma(0))=f(x+tu)-f(x)$
- $\lim_{ t \to 0 } \frac{f(x+tu)-f(x)}{t}=\lim_{ t \to 0 }\frac{g(t)-g(0)}{t}=g’(0)=(\nabla f)(x)\cdot u$
- 注意这里 $\gamma$ 设计,称作沿着向量u方向的方向导数,记作 $(D_{u}f)(x)$
- 如果固定f,x ,变动u,那么u和 $(\nabla f)(x)$方向一致时 值最大,(当然梯度可能为0)
- $u=\sum u_{i}e_{i}$
- $(D_{u}f)(x)=\sum_{i=1}^n (D_{i}f)(x)u_{i}$
9.19 f把凸开集$E \subset R^n$映入$R^m$内, f在E内可微,并有对每个$x\in E$使得
- $||f’(x)|| \leq M$有存在的M, 那么$|f(b)-f(a)| \leq M|b-a|$
- $\gamma(t)=(1-t)a+tb$
- 凸, $\gamma(t)\in E$
- $g(t)=f(\gamma(t))$
- $g’(t)=f’(\gamma(t))\gamma’(t)=f’(\gamma(t))(b-a)$
- $|g’(t)|\leq ||f’(\gamma(t))|| |b-a| \leq M|b-a|$
- 根据5.19 $|f(b)-f(a)|=|g(1)-g(0)|\leq (1-0)|g’(t)|\leq M|b-a|$
- 推论, 如果一切$x\in E$有$f’(x)=0$ 那么$f$是常值函数
9.20 定义 f是$E \subset R^n$到$R^m$内的可微映射, 如果$f’$是把E 连续的 into $L(R^n,R^m)$,那么称f在E内连续可微 continuously differentiable
- 更明确, $|x-y|<\delta$时 $||f’(y)-f’(x)||<\epsilon$
- $f$是$\mathscr{C}’$-mapping 或 者$f\in \mathscr{C’}(E)$
9.21 f的所有偏导数在E上存在且连续 <=> $f\in \mathscr{C}’(E)$
- 证明
- <=
- 根据9.17 $(D_{j}f_{i})(x)=(f’(x)e_{j})\cdot u_{i}$
- $|(D_{j}f_{i})(y)-(D_{j}f_{i})(x)| = | (f’(y)-f’(x))e_{j}\cdot u_{i}|$
- $\leq | (f’(y)-f’(x))e_{j}|$
- $\leq ||f’(y)-f’(x)||$ 这个 是可被控制的,那么 $D_jf_i$也是可以被控制的 连续
- =>
- 只考虑m=1的情况(因为 m有限, 每个维度 如果都连续(可被控制距离),那么 norm下 也可以被控制距离)
- $|(D_{j}f)(y)-(D_{j}f)(x)|< \frac{\epsilon}{n}$
- $h=\sum h_{j}e_{j}, |h| < r$
- $v_0, v_k=\sum_{i=1}^{k} h_{i}e_{i}, |v_{k}|< r$
- $f(x+h)-f(x)=\sum_{j=1}^{n} [f(x+v_{j})-f(x+v_{j-1})]$, S是凸的,所以 可以取到位于球内
- $f(x+v_j)-f(x+v_{j-1})=f’(x+v_{j-1}+\theta_{j}h_{j}e_{j})h_{j}e_{j}=(D_{j}f)(x+v_{j-1}+\theta_{j}h_{j}e_{j})h_{j}$
- $|f(x+h)-f(x)-\sum_{j=1}^n h_{j}(D_{j}f)(x)|\leq \frac{1}{n}\sum_{j=1}^n |h_{j}|\epsilon \leq |h| \epsilon$
凝缩原理 the contraction principle
中断 微分的讨论
在任何完备度量空间都有效的 不动点定理
反函数定理的证明中用到
9.22 X是度量为d的度量空间, $\phi$ 把X映入X内,并且存在 $c< 1$, 对一切x,y有$d(\phi(x),\phi(y))\leq cd(x,y)$
- 那么称$\phi$是X到X内的一个凝缩函数,(is said to be a contraction of X into X)
9.23 X是完备度量空间, $\phi$是X到X内的凝缩函数,那么存在着唯一合于$\phi(x)=x$的$x\in X$
- 换句话 phi 有唯一不动点,唯一性 显然,否讨论这两点的 距离 不满足上述 $d(\phi(x),\phi(y)) \leq cd(x,y)$
- 存在性,任意点$x_{0}$, 构造点列$x_{n+1}=x_{n}$
- 相邻距离 <= c 上一个相邻距离 <= $c^n$ 最初相邻距离
- $d(x^n,x^m) \leq 关于c的等比和 * 最初距离$ 显然有限,而等比的首项,可以通过N控制
- 点列收敛
- 柯西序列,X完备,存在x = lim X_n
- phi 在X上连续(一致连续),所以 f(x)=lim f( X_n)=lim X_{n+1}=x
反函数定理 The inverse function theorem
粗略的说,反函数定理说的是,一个连续可微映射f,在使线性变换f’(x)可逆的点x的邻域内是可逆的
9.24 f把开集E subset $R^n$映入$R^n$内的$\mathscr{C}’$映射, 对于某个a in E, f’(a)可逆,且b=f(a) 那么
- $R^n$存在开集U及V,使得a in U, b in V, f在U上是1-1的,且f(U)=V
- 若g是f的逆,在V内由 g(f(x))=x确定,那么$g \in \mathscr{C}‘(V)$
- 注意 这里,x,y是n维向量
- 证明 写成分量形式,限制在a和b的足够小的邻域内,这样能用y_i把x_i接出来,这组解是唯一的,且是连续可微的
- 令 f’(a)=A, 选取 lambda使得 $2 \lambda ||A^{-1}||=1$
- 因为f’在a连续,必有以a为中心的开球 U subset E,使得 $||f’(x)-A|| < \lambda$ 勘误中文书这里有个莫名其妙的 导数符号
- 这里用的是 9.8 ||B-A|| ||A^{-1}|| < 1 且A可逆,则 B可逆,这里 通过 ||f’(x)-A|| ||A^{-1}|| < lambda ||A^{-1}|| = 1/2 < 1 来完成前提条件
- 再用f’连续,可逆集是开集所以可逆邻域内都可逆,来取得邻域内的U, (这里lambda 这里有点多于后面会用到
- 给每个y 配置一个函数$\varphi(x)=x+A^{-1}(y-f(x))$
- 注意 f(x)=y当且仅当x是$\varphi$的不动点
- 因为$\varphi’(x)=I-A^{-1}f’(x)=A^{-1}(A-f’(x))$
- $||\varphi’(x)||\leq \frac{1}{2}$
- 根据9.19 有$|\varphi(x_{1})-\varphi(x_{2})|\leq \frac{1}{2} |x_{1}-x_{2}|$
- 满足凝缩原理的 <= 的前提条件,所以至多一个不动点 $\varphi(x)=x$ 也就是$y=f(x)$,是1-1映射
- 换句话说 如果f(x) 不是1-1映射,那么 如果两个x映射到同一个y,在那个y对应 $\varphi_y$ 下 这两个点 都是$\varphi_{y}$的不动点
- $V=f(U)$, 取$x_{0}\in U$, $y_{0}=f(x_{0})$, B 是半径$r < r_{U}$,$x_0$为中心的开球
- B的闭包一定在U内
- 目标证明V开集,也就是 只要 $|y-y_{0}|< \lambda r$就必定$y \in V$
- 取定y
- $|\varphi(x_{0})-x_{0}|=|A^{-1}(y-y_{0})| < ||A^{-1}|| \lambda r =\frac{r}{2}$
- 对于 $x \in \bar{B}$ 有 $|\varphi(x)-x_{0}|\leq|\varphi(x)-\varphi(x_{0})|+|\varphi(x_{0})-x_{0}| < \frac{1}{2} |x-x_{0}|+\frac{r}{2}\leq r$ 因此$\varphi(x) \in B$
- 满足 凝缩原理的 自身 到 自身的条件
- 结合上面两个, $\varphi$ 是凝缩函数, $\bar{B}$作为$R^n$的闭子集,必是完备集,存在$\varphi_{y}$的不动点, 而这个不动点x,$f(x)=y$
- $y \in f(\bar{B}) \subset f(U)=V$ 也就是V是开集,综上 1-1映射 以及 U,V都是开
- 性质二的证明:
- y in V, y+k in V, x in U, x+h in U 且 y+k=f(x+h)
- $\varphi(x+h)-\varphi(x)=h+A^{-1}[f(x)-f(x+h)]=|h-A^{-1}k|\leq \frac{1}{2} |(x+h)-x|=\frac{1}{2} |h|$
- 因此 $|A^{-1}k| \geq \frac{1}{2} |h|$
- $|h| \leq 2 ||A^{-1}|| |k| =\frac{1}{\lambda} |k|$
- 上面有$f’(x)$有逆,记作B (这个B 是 线性代数意义里的 逆矩阵也就是 $f’(x)B=I$
- $\frac{|g(y+k)-g(y)-B|}{|k|}=\frac{|h-Bk|}{|k|}=\frac{|(Bf’(x))h-B(f(x+h)-f(x))|}{|k|}=\frac{|-B(f(x+h)-f(x)-f’(x)h)|}{|k|}$
- $\leq \frac{||B||}{\lambda} \frac{|(x+h)-f(x)-f’(x)h|}{|h|} \to 0$
- 证明了 逆函数的导数 = 原函数导数的逆矩阵: $g’(y)=T$
- 也就是 导数的矩阵,从矩阵的逆,与逆函数的导数 之间得到的是同样的矩阵
- 最后 g是 把V映满U的连续映射(因为g可微),
- f’是U到L的所有可逆元集 中的连续映射
- $g\in \mathscr{C}’(V)$
9.25 f是开集E subset $R^n$到$R^n$内的$\mathscr{C}’$映射, $f’(x)$在每个$x \in E$ 可逆,对于每个开集$W \subset E$, $f(W)$是$R^n$的开子集
- 换句话说 f是E到$R^n$内的开映射
- 因为每个x可逆,有邻域 是1-1的,局部1-1的,
隐函数定理 the implicit function theorem
如果f是 plane 平面上 连续可微实函数,函数 f 在点$(a,b)$满足 $f(a,b)=0$
- 且 $\frac{\partial}{\partial y}(f) \neq 0$
- 那么在(a,b)的某个邻域内, 方程 f(x,y)=0 能把y用x解出
- 类似的 $\frac{\partial}{\partial x}f \neq 0$
- 就能在(a,b) 附近把x解出,用y表示
- 这里偏导不等于0的必要,可以考虑 $f(x,y)=x^2+y^2-1$作为例子
9.26 $x \in R^n, y \in R^m$
- $(x,y) \in R^{n+m}$ 向量拼接
- $A(h,k)=A_{x}h+A_{y}k$
- $A \in L(R^{n+m},R^n)$
- $A_{x}\in L(R^n,R^n)$
- $A_{y}\in L(R^m,R^n)$
9.27 若 $A_{x}$可逆, 那么 每个$k \in R^m$ 有唯一h使得 $A(h,k)=0$
- $h=-(A_{x})^{-1}A_{y}k$ 计算出
- 证明: 线性代数的解情况的知识
9.28 f 是开集$E \subset R^{n+m}$ 到$R^n$ 内的$\mathscr{C}’$映射,在某点(a,b) in E使得 f(a,b)=0
- 令 $A=f’(a,b)$, 且假定$A_x$可逆
- 存在开集 $U \subset R^{n+m}$及 $W \subset R^m$, 有$(a,b) \in U,b\in W$ 有以下性质
- 对于每个W中y,有唯一x 使得 (x,y) in U 且 f(x,y)=0,
- 把这些映射定义称 g(y),那么 g是W到$R^n$内的$\mathscr{C}’$ 映射, $g(b)=a$
- $f(g(y),y)=0$
- $g’(b)=-(A_x)^{-1}A_y$
- $f(x,y)=0 \in R^n$ 可以写成含有n+m个变量的n个方程组的方程
- A_x可逆的假定,意味 在(a,b)的值确定 $R^n$ 内的一个可逆线性算子
- 证明:
- 定义 F(x,y) = (f(x,y),y)
- 那么 F是把E映射到 $R^{n+m}$内的$\mathscr{C}’$ 映射, we claim that(断定) F’(a,b)是 可逆
- 因为 f(a,b)=0 所以 f(a+h,b+k)=A(h,k) + r(h,k)余项
- F(a+h,b+k)-F(a,b)=(f(a+h,b+k),k)
- =(A(h,k),k)+(r(h,k),0) 右边这块,根据 余项的 趋于0的 性质判断 也是 余项
- 所以 F’(a,b)是R^{n+m}上的线性算子,它把(h,k)映射成 (A(h,k),k)
- 如果 它是0向量,那么 A(h,k)=0 且 k=0
- 而9.27 说明 h=0
- 因此 F’(a,b)是1-1的也是可逆的 (9.5 线性变换的 核 只有0,那么 为1-1的)
- 那么 可以对F(导函数连续 + 点 导函数可逆)使用反函数定理 得到 (a,b) in U, (f(a,b)=0,b) in V, F把U映满V,且1-1
- 注意 这里 U,V都是上面 9.24 的邻域,并不是所有 (0,b) 构成的集合!,因为显然的 所有(0,b)构成的集合不是开集,因为邻域半径 会让前面0有非零的 点
- 下面找 W, 令W是 适合$(0,y) \in V$的一切$y \in R^m$的集,注意$b\in W$
- 开集:V开集 显然 W开
- 存在性:W中的每个y,存在 (x,y) in U, (0,y)=F(x,y) 这个x使得 f(x,y)=0
- 唯一性:若 同一个y,还有 $f(x_{1},y)=0$, 那么能推得 F中也相等,而F是1-1的说明 只存在唯一的x
- 具体表达式:
- 对于 y in W, 定义 g(y) 使得 g(y),y in U, f(g(y),y)=0
- 于是 F(g(y),y)=(f(g(y),y),y)=(0,y)
- 令G是V映满U的映射,且是F的逆,$G \in \mathscr{C}’$
- (g(y),y)=G(0,y) 我们用“同样的 对应关系“的G 但缩减了值域,而这样的G和新定义的g是同样的映射,所以g也 $g \in \mathscr{C}’$
- 令 $\Phi(y)=(g(y),y)$
- $\Phi’(y)k=(g’(y)k,k)$
- W中 $f(\Phi(y))=f(g(y),y)=0$
- $f’(\Phi(y))\Phi’(y)=0$ 常函数导数为0
- y=b时, $\Phi(y)=(a,b)$ 且 $f’(\Phi(y))=A$ 所以$A\Phi’(b)=0$
- 对于$R^m$中每个k 有 $(A_{x}g’(b)+A_{y})k=A_{x}g’(b)k+A_{y}k=A(g’(b)k,k)=A\Phi’(b)k=0$
- 对于 y in W, 定义 g(y) 使得 g(y),y in U, f(g(y),y)=0
写成f,g的分量形式
- $\sum_{j=1}^{n} (D_{j}f_{i})(a,b)(D_{k}g_{j})(b)=-(D_{n+k}f_{i})(a,b)$
- $\displaystyle \sum_{j=1}^{n} (\frac{\partial f_{i}}{\partial x_{j}})(\frac{\partial g_{j}}{\partial y_{k}})=-(\frac{\partial f_{i}}{\partial y_{k}})$
- 以$\frac{\partial g_{j}}{\partial y_{k}}$ 为为质量,有n个线性方程组
9.29 例子:来个例子感受一下
- n = 2, m = 3
- $f_{1}(x_{1},x_{2},y_{1},y_{2},y_{3})=2e^{x_{1}}+x_{2}y_{1}-4y_{2}+3$
- $f_{2}(x_{1},x_{2},y_{1},y_{2},y_{3})=x_{2}\cos x_{1}-6x_{1}+2y_{1}-y_{3}$
- $f=(f_{1},f_{2})$即$f(x,y)=(f_{1}(x,y),f_{2}(x,y))$
- a=(0,1),b=(3,2,7)
- 带入得此时 f(a,b)=0
- 关于标准基,A=f’(a,b)的矩阵为
- $[A]=\left[ \frac{\partial}{\partial x_{i}}(f_{j}) \frac{\partial}{\partial y_{i}}(f_{j}) \right]$
- $[A]=\left[2e^{x_{1}},y_{1},x_{2},-4,0;-x_{2}\sin x_{1}-6;\cos x_{1},2,0,-1 \right]|_{(x,y)=(a,b)}$
- $[A]=\left[2,3,1,-4,0;-6,1,2,0,-1 \right]$
- $[A_{x}]=[2,3;-6,1]$ 列向量无关,可逆,
- 在b某个邻域存在 $\mathscr{C}’$的g 使得 $g(b=(3,2,7))=a=(0,1)$且$f(g(y),y)=0$
- $[(A_{x})^{-1}]=[A_{x}]^{-1}=\frac{1}{20}[1,-3;6,2]$
- $h=\frac{\partial}{\partial y_{i}}(g_{j})|{y=b} k=g’(b)k=-[A{x}^{-1}A_{y}]k=\left[ \frac{1}{4}, \frac{1}{5}, - \frac{3}{20}; - \frac{1}{2}, \frac{6}{5}, \frac{1}{10} \right] k$
- 这样我们求得了 g在b点邻域里 关于y的偏导值
秩定理 the rank theorem
虽不如 反函数 和 隐函数 重要
我们也把它算作是 连续可微映射 F在一点x的局部性质,与线性变换F’(x)在x点附近的局部性质相似,
9.30 A in L(X,Y), null space of A(零空间) 记作 $\mathscr{N}(A)$, 是使Ax=0的所有组成的集,显然 $\mathscr{N}(A)$ 是X中的向量空间
- A的值域(range of A) $\mathscr{R}(A)$ 是Y中的向量空间
- A 的 秩rank定义为 $\mathscr{R}(A)$的维数
- $L(R^n)$的可逆元,恰好是那些为n的元, 恰好是那些秩为n的元(定理9.5)
- 如果 A的秩是0,那么一切x ,Ax=0, A的零空间是X全体
9.31 projections 射影,投影, 如果 $P^2=P$ 幂等,就说P是X里的摄影
- 更明确说 任意x, 有 P(Px)=Px
- P把每个向量固定在它的值域$\mathscr{R}(P)$中
- 性质:
- P是投影,那么X中每个x能唯一拆解称来自 $\mathscr{R}(P),\mathscr{N}(P)$中的两个向量之和
- x_1 = Px
- x_2 = x-x_1 in Null(P)
- Px_2=Px-Px_1=Px-PPx=0
- 唯一性 证明以下x_1唯一性就好了,
- 对于任意拆分,x_1是在投影里,有Px_1=x_1
- $Px=Px_1+Px_2=x_1+0$
- x_1只能为Px
- X是有限维向量,X_1 是X内的一个向量空间,那么在X中存在着P, $\mathscr{R}(P)=X_{1}$
- 也就是有恰好投影到 指定子向量空间的
- 0维显然
- 根据9.3 在X_1任意选一组基,在X中扩充到X的基
- 那么 P(X中的坐标,按照X中扩充基 分解)=只留X_1中的基
9.32 m,n,r 非负整数 $m \ge r$ , $n \ge r$, F把开集$E \subset R^n$ 映入 $R^m$ 内的 $\mathscr{C}’$ 映射, 对于每个$x \in E$ , $F’(x)$的秩是$r$
- 固定$a \in E$, 令$A=F’(a)$, 设A的值域是$Y_1$, P是$R^m$中的射影,其值域也是$Y_{1}$, $Y_{2}$是P的零空间
- 那么 $R^n$中存在着 开集 U及V, $a \in U \subset E$, 并且存在着把映满U的1-1 $\mathscr{C}’$映射H(onto 逆也是 $\mathscr{C}’$), 使得
- $F(H(x))=Ax+\varphi(Ax), x \in V$ 其中$\varphi$是把 $A(V) \subset Y_1$映入 $Y_2$内的 $\mathscr{C}’$映射
证明:
- 若 r=0, 那么 $F’(x)=0$对一切x成立,那么F是常函数,显然
- a的某领域U内
- 这时 V=U, H(x)=x, $\varphi(0)=F(a)$
- $F(H(x))=F(x)=0+\varphi(0)=F(a)$
- 若 r>0, $\dim Y_1 = r$, $Y_1$有基 {$y_1,…,y_r$}, A可逆,因此选$R^n$中的r个基$z_1,…,z_r$使得$Az_i=y_i$
- 因此 A的’逆’有 $A^{-1}(\sum c_i y_i)=\sum c_i z_i$
- 书上这里是S,来表示这个逆运算,需要注意的是A这里是f’(a) 它甚至可能不是方阵,然后我们这里$S=A^{-1}$, 而我们能做的是什么,其实就是秩为r的矩阵,完成了 行空间 到 列空间的 1-1 的r维映射,所以这里S我们只是这个1-1映射的逆向而已,那么
- $A^{-1}$的 接受的参数 只有列空间$Y_1$中的!!!
- 再细致的
- $AA^{-1}y=y,y\in Y_1$, 这是成立的
- $A^{-1}Ax =?=x , Ax\in Y_1$, 这是不一定的, 因为x可能不在行空间里
- $G(x)=x+A^{-1}P[F(x)-Ax],x\in E$, 这是一个E到$R^n$内的$\mathscr{C}’$映射
- $G’(x)=I+A^{-1}P[F’(x)-A]$
- $G’(a)=I+A^{-1}P[F’(a)-A]=I+A^{-1}P[0]=I$ 恒等算子
- 由于G是1-1的,根据反函数定理 所以G是U到$R^n$内V的1-1 $\mathscr{C}’$映射, G的逆$H=G^{-1}$也是$\mathscr{C}’$
- 因为PA=A,所以 $AA^{-1}PA=A$
- $AG(x)=Ax+P[F(x)-Ax]=PF(x),x \in E$
- $PF(H(x))=AG(H(x))=Ax,x\in V$
- 定义$\Psi(x)=F(H(x))-Ax,x \in V$
- $P\Psi(x)=0$ 所以$\Psi(x) \in Y_2$
- 因为V是开集,显然A(V)是它的值域 $R(A)=Y_1$的开子集
- 下面要证明 存在$A(V)$到$Y_2$的$\mathscr{C}’$映射$\varphi$
- $\varphi(Ax)=\Psi(x),x\in V$
- 若$x_1,x_2\in V, Ax_1=Ax_2$ 那么 $\Psi(x_1)=\Psi(x_2)$
- 证明
- $\Phi(x)=F(H(x)),x \in V$ 因为对于每个$x \in V$, $H’(x)$的秩是n, 对于每个$x \in U$, $F’(x)$的秩是r
- $\Phi’(x)$的秩 = $F’(H(x))H’(x)的秩=r$
- 固定$x \in V$, 令$M$是$\Phi’(x)$的值域, 那么$M \subset R^m,\dim M=r$,
- 根据上面 $P\Phi’(x)=A$
- 因此P把M 映满 $\mathscr{R}(A)=Y_1$, 因为M与$Y_1$同维,所以P(在M上时)是1-1的
- 设$Ah=0$, 于是 $P\Phi’(x)h=0$, 但$\Phi’(x) h \in M$且P在M上是1-1的,所以$\Phi’(x)h=0$
- 即 如果$x\in V$且$Ah=0$那么$\Psi’(x)h=0$
- 令$h=x_2-x_1$,且定义$g(t)=\Psi(x_1+th), 0\le t \le 1$
- V凸的(如果不是可以缩小成凸的),所以$g’(t)=\Psi’(x_1+th)h=0, x_1+th\in V$
- 所以$\Psi(x_1)=g(0)=g(1)=\Psi(x_2)$
- 上面的性质说明 $\Psi(x)$的值 可以只依赖于$Ax$ 因此定义$\varphi(Ax)=\Psi(x)$ 是函数
- 接下来证明$\varphi$是$\mathscr{C}’$
- 固定$y_0\in A(V)$再固定$x_0\in V$使$Ax_0=y_0$ 因为V是开集, $y_0$必在$Y_1$中有邻域W,凡是$y\in W$时 $x=x_0+A^{-1}(y-y_0) \in V$
- $Ax=Ax_0+AA^{-1}(y-y_0)=y$
- $\varphi(y)=\varphi(Ax)=\Psi(x)=\Psi(x_0+A^{-1}(y-y_0)), y \in W$
- 这说明W中$\varphi \in \mathscr{C}’$
- 由于$y_0$是任意的,所以$\varphi$是$\mathscr{C}’$
- 证毕
- 因此 A的’逆’有 $A^{-1}(\sum c_i y_i)=\sum c_i z_i$
知乎: https://zhuanlan.zhihu.com/p/694698914
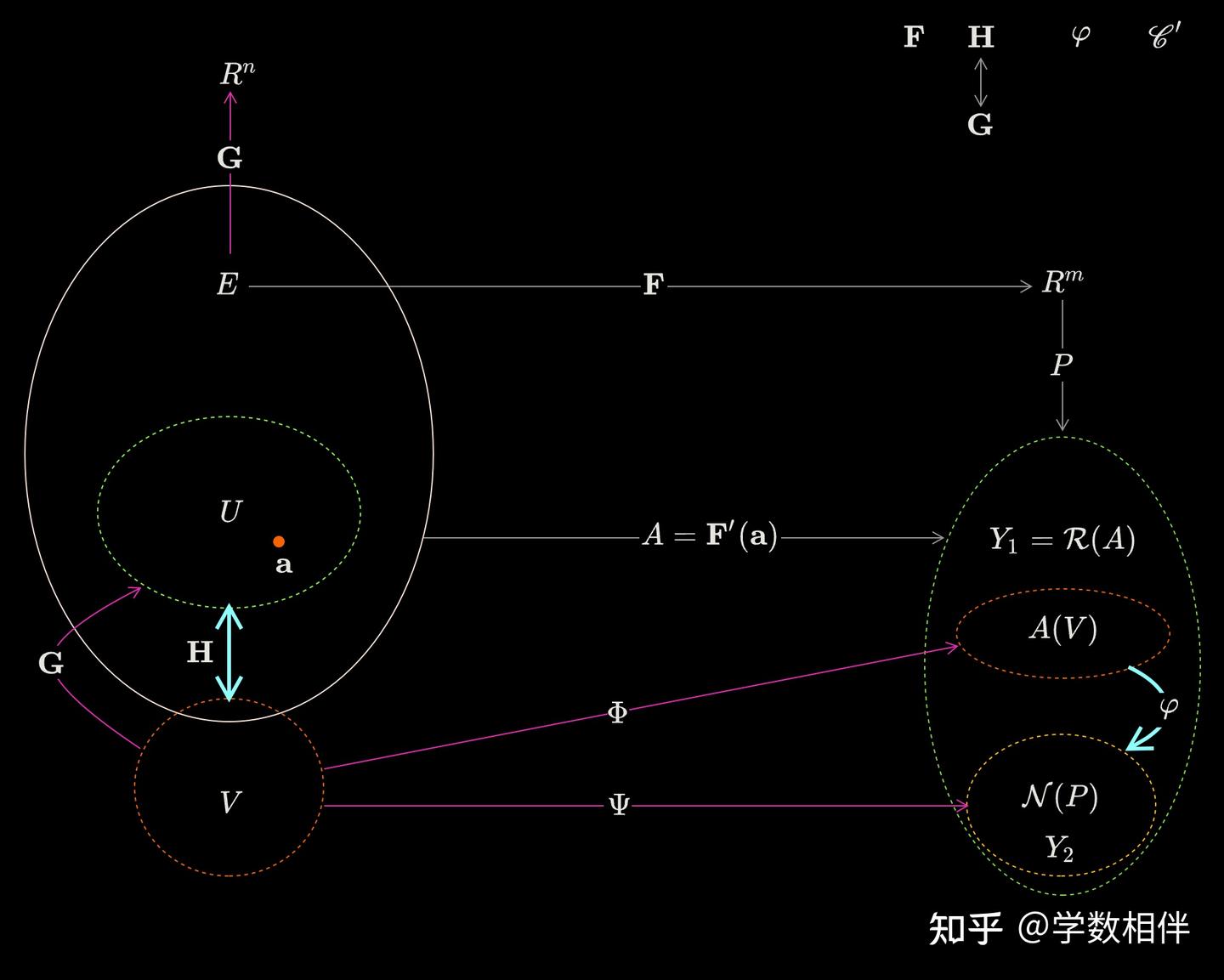
图感觉不完全对
- G,H是互逆的,G: U->V, H: V->U
- $A=F’(a)$,但是映射的是$R^n$ 到$Y_1$,
- 其中 A的逆$S=A^{-1}$ 是 $Y_1 \to R^n$中的r维A的行空间
- $Y_1,Y_2$应该画成正交形式的
来说一说 关于映射F的几何意义
- 如果$y \in F(U)$那么有某个$x\in V$,使得$y=F(H(x))$
- $Py=Ax$
- $y=Py+\varphi(Py), y\in F(U)$
- 说明y被它的投影所确定
- 如果把P限制在F(U)内,P就是把F(U)映满A(V)的1-1映射
- 因此$F(U)$是r维曲面surface,在A(V)的每个点的 上面 恰好有一个F(U)的一个点,也可以把F(U)当成$\varphi$的图像
- 如果像证明中那样$\Phi(x)=F(H(x))$那么说明$\phi$的水平集 level sets(在这个集上,Phi的值是一个给定的值attains a given value)恰好是A在V中的水平集,这些集(A的水平集)都是平坦flat的,因为他们都是向量空间Nullspace(A)的平移与V的交
- dim N(A)=n-r
- F在U中的水平集level sets,是Phi在V中的平坦水平集在H之下的像,于是它们是U中的n-r维曲面
$F(x)=AG(x)+\varphi(AG(x)), x \in U$
- G: U到V的1-1映射, E到$R^n$内的$\mathscr{C}’$映射
- $\varphi$是$A(V)$到$Y_2$的$\mathscr{C}’$映射
- G怎么来的:
- 这样想, $F:E\to R^m$, 那么拆解值域成 正交结构
- $F(x)=PF(x)+(F(x)-PF(x))$
- 左边 PF(x)在$Y_1$中,右边的括号在$Y_2$中
- 另一方面希望 $F(x)=F(a)+F’(a)(x-a)+r(x-a)$ 同样按照正交拆解
- $F(x)=A(x-a+A^{-1}PF(a))+(F(a)-PF(a)) + r(x-a)$
- 这里出现了A的逆,要合理化就是 去找对应的1-1的r维映射的逆
- 注意同上,$A^{-1}$只能接受$Y_1$中的元素
- 所以$G(x)=x-a+A^{-1}PF(a)$这样的形式, 一方面我们希望$AG(x)=PF(x)$ 同样的正交分解部分相等
- 这里神奇的一点就是 $Aa = AA^{-1}PAa$
- $G(x)=x-A^{-1}PAa+A^{-1}PF(a)$
- $G(x)=x+A^{-1}P(F(a)-Aa)$ 结构上就和上面一样了, 而这里a换成x满足 $AG(x)=PF(x)$,
- 这样想, $F:E\to R^m$, 那么拆解值域成 正交结构
- $\varphi$的部分
- 根据拆解 $F(x)-PF(x)=\varphi(AG(x))$,希望这个成立
- 到 nullspace(P)的 $Y_2$是显然的,因为 拆解就是 正交拆解
- 那么 只和 $AG(x)$有关,和$\mathscr{C}’$这两个证明,
- 后一个的感官上更显然,F,P,A,G 都是 ,这里是复合运算
- 前一个,$F(x)-PF(x)$,注意到$PF(x)=AG(x)$,所以需要证明的是 $F(x)$只和$AG(x)$有关, F(x)只和x有关,A可逆,G可逆,所以F只和AG(x)
- 其中G可逆,需要反函数定理
行列式 determinants
行列式与方阵有关的数,行列式是0的充要条件是相应的算子不可逆
9.33 如果($j_1,…,j_n$)是正整数的有序n元组(有序的n个正整数
- $s(j_1,…,j_n)=\prod_{p<q} sgn(j_q-j_p)$
- 右边是符号函数
- 换句话说 是 -1的 逆序对个数的幂次
- 设[A]是$R^n$上线性算子A关于标准基的矩阵, i行j列 阵元是 $a(i,j)$,
- 定义 $\det[A]=\sum s(j_1,\cdots,j_n)\prod a(i,j_i)$
- 遍历所有$j_i$的排列方法
- 把[A]表示成列向量 $[A]=(x_1,\cdots,x_n)$
- 那么$\det [A]=\det(x_1,\cdots,x_n)$ 是一个实函数
- 定义域是 $R^n$中一切有序n元组所组成的集
9.34
- I是恒等算子,$det[I]=det(e_1,\cdots,e_n)=1$
- 如果$x_j$外其它列向量保持不变, det便是$x_j$的线性函数
- det[A]=-det[A交换某两列]
- [A]如果两列相等那么 det[A]=0
- 这个在MIT的线代课程里面,前三条是定义,而9.33是靠这三条推出的公式,这里第4条 完全可以由2,3 条得到
- 这里是9.33 是定义,而要推这些性质,这个两个角度看,前三条也是可以看做核心性质了
9.35
- $\det([B][A])=\det[B]\det[A]$
- 证明:
- 定义 $\Delta_B(a_1,\cdots,a_n)=\Delta_B[A]=\det([B][A])=\det(Ba_1,\cdots,Ba_n)$
- 因此$\Delta_B$也有9.34的2-4条性质,可以把$a_i$拆解成标准基的表示,并利用线性性拆出
- $\Delta_B[A]=\sum (\prod a(i_j,j)) \Delta_B(e_{i_1},\cdots,e_{i_n})$
- 其中右侧 $\Delta_B(e_{i_1},\cdots,e_{i_n})=t(i_1,\cdots,i_n)\Delta_B(e_1,\cdots,e_n)=t(i_1,\cdots,i_n)\det[B]$
- 这里t需要 里面是1~n的某个排列 才非零,是1或-1, 而当非0时,对应的是$s(i_1,\cdots,i_n)$
- 和前面结合即是 $\det[A]$
9.36 定理 $R^n$上的线性算子A可逆的充要条件是 $\det[A]\neq 0$
- 可逆 $\det[A]\det[A^{-1}]=\det[AA^{-1}]=\det[I]=1$ 所以一定不为0
- 不可逆, 列线性相关(定理9.5), 因此有一列可被其它列表示,构造变换值不变 = 0
9.37 评注, e,u都是基, 每个线性算子(MIT叫线性变换),能确定两个方阵$[A],[A]_U$,
- $Ae_j=\sum_i a_{ij}e_i$
- $Au_j=\sum_i c_{ij}u_i$
- 来确定它们的阵的元素 $a_{ij},c_{ij}$
- 如果$u_j=Be_j=\sum_i b_{ij}e_i$, 那么
- $Au_j=\sum_k c_{kj}u_k=\sum_k c_{kj}Be_k=\sum_k c_{kj}\sum_i b_{ik}e_i=\sum_i (\sum_k b_{ik}c_{kj})e_i$
- $Au_j=ABe_j=A\sum_k b_{kj}e_k=\sum_i (\sum_k a_{ik}b_{kj})e_i$
- 所以 $\sum_{k} b_{ik}c_{kj}=\sum_k a_{ik}b_{kj}$ 因为上面是分解的正交基
- 即 $[B][A]_U=[A][B]$
- B可逆, $\det[B]\neq 0$,
- $\det[A]_U=\det[A]$
- 因此 线性算子 的矩阵 的行列式,与构成的基无关,所以可以称作线性算子的行列式
- 这里MIT里的 一个是变换,而一个变换的指定基下的矩阵 的行列式,还是在描绘 这个基下各个 基向量的拉伸放缩翻转的整体情况
9.38 函数行列式, f把开集$E\subset R^n$映入$R^n$内,并且f在点$x\in E$ 可微, 线性算子 f’(x) 的行列式,叫做f在x的函数行列式 记作
- $J_f(x)=\det f’(x)$
- 若 $(y_1,\cdots,y_n)=f(x_1,\cdots,x_n)$ 又可以用记号
- $\frac{\partial(y_1,\cdots,y_n)}{\partial(x_1,\cdots,x_n)}$
- 在反函数定理中, 需要的就是$J_f(x)\neq 0$
高阶导数 derivatives of higher order
9.39 定义 f是定义在开集 $E\subset R^n$的实函数, 其偏导数是$D_1f,\cdots,D_nf$如果, 每个$D_jf$也可微,那么f的二阶偏导数定义为
- $D_{ij}f=D_iD_jf$
- 如果所有这些$D_{ij}f$都在E内连续, 就说 f在 E内属于 $\mathscr{C}’’$ 类,或者$f\in \mathscr{C}’’(E)$
- 对于向量映射,如果$f:R^n\mapsto R^m$ 每个分量都是$\mathscr{C}’’$类的,就说$f$属于$\mathscr{C}’’$类的
- 注意的是,习题27,即使$D_{ij}f$和$D_{ji}f$都存在,也不一定相等,但是如果它们都连续,那么它们一定相等
- 习题27: $f(x,y)=\frac{xy(x^2-y^2)}{x^2+y^2}$, 其中在(0,0)补充定义为0
9.40 定理 设f定义在开集 $E\subset R^2$中,并且$D_1f$及$D_{21}f$在E的每个点处存在,设$Q\subset E$是闭矩形,它的边与坐标轴平行,并且$(a,b)$及$(a+h,b+k)$是它的opposite vertices, $h\neq 0,k \neq 0$
- 令 $\Delta(f,Q)=f(a+h,b+k)-f(a+h,b)-f(a,b+k)+f(a,b)$
- 那么Q内存在一点$(x,y)$使 $\Delta(f,Q)=hk(D_{21}f)(x,y)$
- 注意到 hk = Q的面积,而上面定义的意义是 x=a+h位置的值变化 减去 x=a位置的值变化?或者是y=b+k位置的值变化 减去 y=b位置的值变化
- 证明:
- 令 $u(t)=f(t,b+k)-f(t,b)$ 也就是在x=t位置的值变化
- $\Delta(f,Q)=u(a+h)-u(a)$
- $=hu’(x)$ 因为 $D_1$存在,以及中值原理
- $=h[(D_1f)(x,b+k)-(D_1f)(x,b)]$
- $=h[k(D_{21}f)(x,y)]$
9.41 设f定义在开集 $E\subset R^2$上,又设$D_1f,D_2f,D_{21}f$在E的每个点上存在,且$D_{21}f$在 点(a,b)连续,那么$D_{12}f$在(a,b)上存在且等
- 证明:
- 令 $A=(D_{21}f)(a,b)$
- 对于任意$\epsilon > 0$如果$Q$是像在定理9.40中那样的矩形, h及k充分小, 那么一切$(x,y)\in Q$有
- $|A-(D_{21}f)(x,y)| < \epsilon$
- $|A-\frac{\Delta(f,Q)}{hk}| < \epsilon$
- 固定h,令$k\to 0$,因为$D_2f$在E中存在, 由上面这个不等式有
- $|\frac{(D_2f)(a+h,b)-(D_2f)(a,b)}{h} - A|\le \epsilon$
- 因为$\epsilon$是任意的, 足够小$h\neq 0$成立的,得证
- 推论 $f\in \mathscr{C}’’(E)$则$D_{21}f=D_{12}f$
积分的微分法 differentiation of integrals
$\varphi$是二元函数, 它对其中一变元可积分,另一个变元可微分,问题是能否交换顺序保持结果相等
- $\frac{d}{dt} \int_a^b \varphi(x,y)dx = \int_a^b \frac{\partial}{\partial t}(\varphi) (x,t) dx$
- 习题28有不等的反例
- $\varphi_t(x)=\varphi(x,t)$记作固定t后的关于x的一元函数
9.42 设
- $a\le x \le b, c\le t \le d$, $\varphi(x,t)$有定义
- 矩形内有定义
- $\alpha$是$[a,b]$上的递增函数
- 相对黎曼可积的前提条件
- 对于$t\in[c,d]$, $\varphi_t \in \mathscr{R}(\alpha)$
- 每个第二个变量固定,第一个变量黎曼可积
- $c < s <d$每个$\epsilon > 0$有$\delta > 0$使得一切$x\in [a,b]$及一切$t \in (s-\delta,s+\delta)$ 有$|(D_2\varphi)(x,t)-(D_2\varphi)(x,s)| < \epsilon$
- 第二个变量的偏导 在 矩形上固定第一个变量后,逐点连续
- 只要$D_2\varphi$在定义$\varphi$的那个矩形上连续,这个就一定成立
- 定义 $f(t)=\int_a^b \varphi(x,t) d\alpha(x), c\le t\le d$
- 第三条 断言一切t,这个积分都存在
- 那么 $(D_2\varphi)_s \in \mathscr{R}(\alpha), f’(s)$存在 并且 $f’(s)=\int_a^b (D_2\varphi)(x,s)d\alpha(x)$
- 证明:
- $\Psi(x,t)=\frac{\varphi(x,t)-\varphi(x,s)}{t-s}$
- 其中$0 < |t-s| < \delta$ 据定理 5.10, 对应于每个$(x,t)$在s与t之间有数u,使得$\Psi(x,t)=(D_2\varphi)(x,u)$
- $|\Psi(x,t)-(D_2\varphi)(x,s)|<\epsilon$
- $t\to s$时, $[a,b]$上有一致地有 $\Psi_t \to (D_2\varphi)_s$,
- 注意 $\frac{f(t)-f(s)}{t-s}=\int_a^b \Psi(x,t) d\alpha(x)$
- 因为每个$\Psi_t \in \mathscr{R}(\alpha)$
- 所以这里核心还是 直接展开 $f’$和$D_2\varphi$ 也就是两个 导的表达来完成证明
9.43 当然也能证明把9.42中 $[a,b]$换成 $(-\infty,\infty)$时所得的类似的定理,只是看个例子
- $f(t)=\int_{-\infty}^{\infty} e^{-x^2} \cos(xt)dx$
- $g(t)=-\int_{-\infty}^{\infty} xe^{-x^2} \sin(xt)dx$
- 其中$-\infty < t \infty$ 两个积分都存在(绝对收敛)
- 注意g是从f把被积式对t微分得来的,我们断定f可微小且 f’(t)=g(t)
- 证明:
- $\beta > 0$那么 $\frac{\cos(\alpha+\beta)-\cos \alpha}{\beta} + \sin \alpha =\frac{1}{\beta} \int_{\alpha}^{\alpha+\beta} (\sin \alpha - \sin t) dt$
- 因为$|\sin \alpha - \sin t | \le |t-\alpha|$,右端绝对值 最大是$\beta / 2$,
- $\beta < 0$时类似处理
- 因此 所有$\beta$, 有$|\frac{\cos(\alpha+\beta)-\cos \alpha}{\beta} + \sin \alpha| \le |beta|$
- 等于0时左侧补充定义为0
- 固定t且固定h, $\alpha = xt,\beta =xh$
- $|\frac{f(t+h)-f(t)}{h}-g(t)|\le |h|\int_{-\infty}^{\infty} x^2 e^{-x^2} dx$, h趋于0时 证明了 $f’(t)=g(t)$
- 再前进一步,f分部积分
- $f(t)=2\int_{-\infty}^{\infty} xe^{-x^2} \frac{\sin(xt)}{t}dx$
- 于是$tf(t)=-2g(t)$也就有微分方程
- $2f’(t)+tf(t)=0$
- 解微分方程以及$f(0)=\sqrt{\pi}$ 有$f(t)=\sqrt{\pi} exp(-\frac{t^2}{4})$