Fermat's two square theorem

發表於 2023-03-13 更新於 2024-10-23 分類於数论 Disqus：文章字數： 8k 所需閱讀時間 ≈ 7 分鐘

Fermat's 两平方数定理:能被表示成平方和的奇素数是所有形如4k+1的奇素数

定理

对于奇素数$p$有能被表示成$p = a^2+b^2$和$p = 4k+1$为充要条件

证明

一定不是$4k+3$

众所周知

$(4k+0)^2 \equiv 0 \pmod 4$

$(4k+1)^2 \equiv 1 \pmod 4$

$(4k+2)^2 \equiv 0 \pmod 4$

$(4k+3)^2 \equiv 1 \pmod 4$

所以

$a^2 + b^2 \not\equiv 3 \pmod 4$

那么有了充分, 如果$p = a^2+b^2$则一定$p = 4k+1$

$p=4k+1 \to p=a^2+b^2$

现在问题剩下就是如果奇素数$p = 4k+1$, 如何证明它可以被表示成$a^2+b^2$

Euler’s proof by infinite descent

如果两个整数都能表示为两个平方数之和，则它们的积也能表示为两个平方数之和

Brahmagupta-Fibonacci Identity

$(a^2+b^2)(c^2+d^2) = (ac+bd)^2 + (ad-bc)^2$

只有$ad=bc$ 时右侧有0的平方 , 也就是两个整数成$c^2/a^2$的倍数

如果一个能表示为两个平方数之和的整数被另一个能表示为两个平方数之和的素数整除，则它们的商也能表示为两个平方数之和

$a^2+b^2 = k (c^2+d^2)$,$(c^2+d^2) = p$为素数

$(cb-ad)(cb+ad) = c^2(a^2+b^2)-a^2(c^2+d^2) = (c^2k-a^2)p$

若$cb-ad$ 是 p 的倍数(另一半假设,对称同理)

$kp^2 = (a^2+b^2)(c^2+d^2) = (ac+bd)^2+(ad-bc)^2$

得到 $ap+bq$ 也是 p的倍数

$k = (\frac{ac+bd}{p})^2+(\frac{ad-bc}{p})^2$ 能表示成整数的平方和

如果一个能表示为两个平方数之和的整数被另一个不能表示为两个平方数之和的整数整除，则它们的商也必有一个不能表示为两个平方数之和的因子

$a^2+b^2 = x \cdot p_1 \cdot p_2 \cdots p_n$ x不能表示为两个数的平方和, 则 $p_i$ 中至少有一个不能表示为两个平方数之和的因子

如果$p_i$ 都能表示成，那么根据上面的结论，必定能表示成平方和，矛盾

如果$a,b$互素，那么$a^2+b^2$ 所有因子都能表示为两个平方数之和

$a^2+b^2 = x \cdot p_1 \cdot p_2 \cdots p_n $

$a = mx \pm c, b = nx \pm d$, 其中 $ 2|c| \leq x,2|d| \leq x$

有 $a^2+b^2 = m^2x^2 \pm 2mxc + c^2 + n^2x^2 \pm 2nxd + d^2 = Ax+(c^2+d^2)$

$c^2+d^2 = kx$

令$g = gcd(c,d)$

因为$\gcd(a,b)=1 \Rightarrow \gcd(a,x)=1 \Rightarrow \gcd(c,x)=1$, 同理 $\gcd(d,x)=1$, 所以$\gcd(g,x)=1$

$g^2((\frac{c}{g})^2+(\frac{d}{g})^2) = kx$, 说明中间的部分也是$x$的倍数

能得到 $e^2+f^2=k_1x$ 且$e,f$互素

$k_1x = e^2+f^2 \leq c^2+d^2 \leq (\frac{x}{2})^2 + (\frac{x}{2})^2 = \frac{x^2}{2}$

有 $k_1 \leq \frac{x}{2}$

由上一个定理，若x非平方和，那么k包含非平方和因子,令这个因子为$x’$

$x’ \leq k_1 \leq \frac{x}{2} < x $

综上如果$a,b$互质,$x$是 $a^2+b^2$ 的因子，且$x$不能被表示成两个数的平方和，那么存在一个小于$x$的数$x’$，也满足是$e^2+f^2$的因子($\gcd(e,f)=1,e\le a,f\le b$),且$x’ < x$小，同时也是不能表示成两个数的平方和。

然而整数无法无限下降，所以所有因子都能表示成两个数的平方和

即若$\gcd(a,b)=1$,那么$a^2+b^2$的质因子只有$2$和$4k+1$形式的

$4n+1$形式的素数是平方分解数

$p = 4n + 1$

$1,2^{4n},3^{4n},…,(4n)^{4n}$ 模$p$余1 (费马小定理)

$2^{4n}-1,3^{4n}-2^{4n},…,(4n)^{4n}-(4n-1)^{4n}$ 均是$p$的倍数

$a^{4n} - b^{4n} = (a^{2n}+b^{2n})(a^{2n}-b^{2n})$

若 $p$ 是任意一个 $a^{2n}+b^{2n}$ 的因子，注意到 $a,p$ 互质, $b,p$互质,$a,b$ 互质（a=b+1）

由上一条引理，$p$ 是互素平方和的因子，所以$p$可以拆解成两个数的平方和

否则 $p$ 是所有 $a^{2n}-b^{2n}$ 的因子

$(x+1)^{2n} - x^{2n} = ((x+1)^n + x^n) ((x+1)^n - x^n)$

差分 $f(x)$ 为$n$次多项式，那么 $f(x)$ 的$n$阶差分为 $n!a_n$

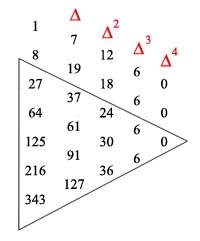
$ f(x) = a_0 + a_1x $

$ f(x+1) - f(x) = a_1 $ 一次多项式得证

若 $n-1$次多项式成立

设 $f$ 是$n$次多项式 $ f(x) = a_0 + a_1x+ \cdots + a_nx^n $

$ g(x) = f(x+1) - f(x) = k_0 + k_1x+ \cdots + a_n \cdot n x^{n-1} $

$g$是 $n-1$次多项式，且其最高项的系数为 $a_n \cdot n $

因为 $g(x)$ 的$n-1$阶差分为 $(n-1)!(a_n \cdot n) = n! a_n$，归纳法递推得证

回到上面我们因为p是所有减法式子的因子，因此$f(x) = x^{2n}$的$2n$阶差分为$(2n)!$, 差分过程中始终是$p$的倍数

而$(2n)!$不是$p$的倍数，所以矛盾。必然$p$是上面某个加法的因子

综上，$4n+1$ 形式的素数是平方分解数

$4n+3$ 根据模4的余数，显然不是

综上充要得证: 一个奇素数是平方分解数，那么它是$4n+1$, 一个素数是$4n+1$形式，那么它是平方分解数

补充性质

$p = x^2+y^2$ 质数唯一表示

$p = a^2+b^2=c^2+d^2$

轮换性质，不妨设$a>c>d>b$

$(ac+bd)(ad+bc) = (a^2+b^2)cd +(c^2+d^2)ab = p(cd+ab)$

至少一个是p的倍数, 若 $(ac+bd) = Kp$ ,

$0 < (a-c)^2+(b-d)^2 = a^2+b^2+c^2+d^2-2ac-2bd = 2p-2Kp < 2p $，

同时除2,$0 < p-Kp < p $ 矛盾

因此$p$ 唯一表示成两个

Lagrange’s proof through quadratic forms

TODO

Dedekind’s two proofs using Gaussian integers

TODO

Proof by Minkowski’s Theorem

TODO

Zagier’s “one-sentence proof”

https://people.mpim-bonn.mpg.de/zagier/files/doi/10.2307/2323918/fulltext.pdf

Roger Heath-Brown in 1971

$p = 1 + 4k$

如果可以拆分，显然一奇一偶

$p = x^2+ (2y)^2 = x^2+4y^2$

考虑

$p = x^2+4yz$

有解$(x,y,z) = (1,1,k)$, 注意到如果 $y\neq z$,那么$(x,y,z)$如果是一组解,则有$(x,z,y)$,形成配对

那么如果能证明$p=x^2+4yz$的所有解的个数是奇数个，那么必定有不能配对的就是$y=z$的, 就是一个解了(这种方法不会直接给到如何计算，但是从存在性上完成证明)

   b
cccb
 dob
 daaa
 d

   b
cooo
 ooo
 oooa
 d

以$x^2$拼o,然后以类似上面形式拼4个$yz$

那么只有

   c
   c
   c
dddobbb
   a
   a
   a

唯一对应$(y,z)$ (因为相当于$y=x$的情况,即$p=x^2+4xz=x(x+4z)$只有$x=1$)

而其它的都对应两个不同的$(y,z)$的解

得证

$x^2+ny^2$

原文见Cox的书

有几个性质(稍后证明):

$p=x^2+y^2, x,y \in \mathbb{Z} \Leftrightarrow p\equiv 1 \pmod 4$

$p=x^2+2y^2, x,y \in \mathbb{Z} \Leftrightarrow p\equiv 1 \mathrm{or} 3 \pmod 8$

$p=x^2+3y^2, x,y \in \mathbb{Z} \Leftrightarrow p=3 \mathrm{or} p \equiv 1 \pmod 3$

$(x^2+ny^2)(z^2+nw^2) = (zx\pm nyw)^2+n(xw\mp yz)^2$

若$N = x^2+ny^2, p | N,p=a^2+nb^2,\gcd(a,b) = 1$, $p$是质数

参考$n=1$时

$(ax-nby)(ax+nby) = a^2x^2-n^2b^2y^2 = a^2(x^2+ny^2) - ny^2(a^2+nb^2) = a^2N - ny^2p$

因此前面至少一个是p的倍数, 不妨设$c=\frac{ax-nby}{p}$,则$d=\frac{bx+ay}{p}$,均为整数

因此如果$N=x^2+ny^2$且有质因子也能表示成$p=a^2+ny^2$,那么$\frac{N}{p}$也可以表示成$c^2+nd^2$

若$N=x^2+ny^2, N = zz’$,而$z$无法被表示成$a^2+nb^2$,则$z’$中有无法被表示成$a^2+nb^2$形式的质因子

反证法, 若$z’$的的所有质数因子都能被表示,根据上面的$\frac{N}{p_1}$能被表示$\frac{N}{p_1p_2}$,这样逐个除$z’$中的质因子,最终$z$也可以被表示矛盾

对于$p | x^2+ny^2,\gcd(x,y)=1$, 因为知道$t^2 \equiv (p-t)^2\pmod p$, 所以可以取$x = min(|x| \bmod p, p - |x| \bmod p) \le \frac{p}{2}$, 对于$y$同理

注意的是，在调整到$\le \frac{p}{2}$的过程中 $\gcd(x,y)=1$可能会不满足,但是注意到$gcd(x,p)=1,gcd(y,p)=1$,即$\gcd(\gcd(x,y),p) = 1$,因此即使过程$\gcd(x,y)\neq 1$,只需要$x,y$同时除以$gcd(x,y)$即可

因此可以取$|x|,|y|\le \frac{p}{2}$ 因为$\gcd(x,y)=1$，只有$x=y=\frac{p}{2} = 1$时才会有同时小于等于取等,也就是$p=2$的特殊q情况

对于一般$p>3$的情况, 则当$n\le 3$时, $x^2+ny^2 < (\frac{p}{2})^2 + n(\frac{p}{2})^2 =\frac{1+n}{4}p^2 \le p^2$时

这就是Fermat的当$p > 3$是$x^2+ny^2$的因子时,可以通过调整$x,y$让$x^2+ny^2 < p^2$

那么有如果$p$不可被表示,则$1 < \frac{x^2+ny^2}{p} < p$且不可被表示,无法无穷下降

综上$x^2+ny^2,n\le 3,\gcd(x,y)=1$时, 它的质因子形式都是$a^2+nb^2$

特殊的

对于$n=2$时，如果$2|x$则考虑$y^2+2(\frac{x}{2})^2$, 最后会递降到3

其中对于$n=3$ 时,如果$3|x$则考虑$y^2+3(\frac{x}{3})^2$,可能有$4$也是因子, 即$4p | x^2+3y^2,gcd(x,y)=1$

但是注意到$x-3y,x+3y$ 至少一个是4的倍数,因此同上面拆的部分可得到$p|x’^2+3y’^2$, 也就是当$x,y$同时为奇数的时候，可以除以$1^2+3\cdot 1^2$来完成下降,直到$p$可以表示或者$x,y$一个奇一个偶数

$p=x^2+ny^2$ and Quadratic Reciprocity

($n=5$时Euler和Fermat都知道这个结论不一定 $21=1^2+5\cdot 2^2, 3|21$,但是$3$不能被表示)

Legendre symbol (a是整数,p是奇质数)

${\displaystyle \left({\frac {a}{p}}\right)={\begin{cases}1&{\text{if }}a{\text{ is a quadratic residue modulo }}p{\text{ and }}a\not \equiv 0{\pmod {p}},\\ -1&{\text{if }}a{\text{ is a quadratic nonresidue modulo }}p,\\ 0&{\text{if }}a\equiv 0{\pmod {p}}.\end{cases}}}$

或者$(\frac{a}{p}) = a^{\frac{p-1}{2}} \pmod p$

对于$1,-1$也就是是否存在$x^2 \equiv a \pmod p$,因为存在时显然$a^{\frac{p-1}{2}} \equiv x^{p-1} \equiv 1 \pmod p$

设$g$为模$p$的一个原根,则存在$k$使$g^k\equiv n \pmod p$,所以$(g^k)^{\frac{p-1}{2}} \equiv 1 \pmod p$, 因为$g$是原根,所以$p-1 | k\cdot \frac{p-1}{2}$, 因此$\frac{k}{2}$是整数,所以$n \equiv (g^{\frac{k}{2}})^2$

综上$x^2 \not\equiv a\pmod p \Leftrightarrow (\frac{a}{p}) = -1$

定理1.7: $n$是非零整数, $p$是奇质数且$p\nmid n$, 则 $p \mid x^2+ny^2,\gcd(x,y)=1 \Leftrightarrow (\frac{-n}{p})=1$

因为$x^2+ny^2\equiv 0 \pmod p, gcd(x,y)=1$ 则$gcd(y,p) = 1$

$x^2 \equiv -ny^2 \pmod p$

$(x^2)^{\frac{p-1}{2}} \equiv (-ny^2)^{\frac{p-1}{2}} \pmod p$

$x^{p-1} \equiv (-n)^{\frac{p-1}{2}}y^{p-1} \pmod p$

$1 \equiv (-n)^{\frac{p-1}{2}}\cdot 1 \pmod p$

正向得证

即存在$z^2 \equiv -n \pmod p$

即$z^2 + n\cdot 1^2 \equiv -n+n \equiv 0 \pmod p, gcd(z,1)=1$

反向得证，充要得证

然后欧拉发现了一些

$(\frac{-3}{p}) = 1 \Leftrightarrow p\equiv 1,7 \mod 12$

$(\frac{-5}{p}) = 1 \Leftrightarrow p\equiv 1,3,7,9 \mod 20$

$(\frac{-7}{p}) = 1 \Leftrightarrow p\equiv 1,9,11,15,23,25 \mod 28$

$(\frac{3}{p}) = 1 \Leftrightarrow p\equiv \pm 1 \mod 12$

$(\frac{5}{p}) = 1 \Leftrightarrow p\equiv \pm 1,\pm 9 \mod 20$, (注这里$\pm 9$也可以写成$\pm 11$,但是$\pm 9$会让人发现都是奇数平方)

$(\frac{7}{p}) = 1 \Leftrightarrow p\equiv \pm 1,\pm 9,\pm 25 \mod 28$

但不是所有都能变成平方，比如

$(\frac{6}{p}) = 1 \Leftrightarrow p\equiv \pm 1,\pm 5 \mod 24$

但6不是质数

若$p$是奇质数,

若$p\equiv 1 \pmod 4, (\frac{-1}{p}) = 1$

若$p\equiv 3 \pmod 4, (\frac{-1}{p}) = -1$

证明 $(\frac{-1}{p}) \equiv (-1)^{\frac{p-1}{2}} \pmod p$, 显然得证

猜想1.9, 如果$p,q$是不同的质数,则$(\frac{q}{p}) = 1 \Leftrightarrow p\equiv \pm \beta^2 \bmod 4q$对于一些奇数$\beta$, (待证明)

命题1.10(重要,也就是而二次互反律quadratic reciprocity) 若$p,q$是不同奇质数,则1.9等价于 $(\frac{p}{q})(\frac{q}{p}) = (-1)^{\frac{(p-1)(q-1)}{4}}$

证明: 显然$(\frac{-1}{p}) = (-1)^{\frac{p-1}{2}}$,$(\frac{ab}{p}) = (\frac{a}{p})(\frac{b}{p})$

????????

Page 27/363

Ref

https://yexiaorain.github.io/Blog/pe/233

https://mathoverflow.net/a/299696/500903

http://www.math.toronto.edu/~ila/Cox-Primes_of_the_form_x2+ny2.pdf

https://nonagon.org/ExLibris/euler-proves-fermats-theorem-sum-two-squares

https://en.wikipedia.org/wiki/Legendre_symbol

https://www.youtube.com/watch?v=VBPrP4nChbo

http://ramanujan.math.trinity.edu/rdaileda/teach/f20/m3341/lectures/lecture18_slides.pdf

https://egrove.olemiss.edu/cgi/viewcontent.cgi?article=2539&context=etd