LarsVAhlfors 复分析 1 复数

isbn

• 中文 9787111703365

• 英文 9787111701026

• 复数 complex numbers

  • 复数代数 the algebra of complex numbers
    • 算术运算 Arithmetric Operations
    • 平方根 Square Roots
    • 合理性 Justification
    • 共轭和绝对值 Conjugation, Absolute Value
    • 不等式 Inequalities
  • 复数的几何表示 the geometric representation of Complex Numbers
    • 几何加法和几何乘法 Geometric Addition and Multiplication
    • 二项方程 The Binomial Equation
    • 解析几何 Analytic Geometry
    • 球面表示 The Spherical Representation
  • TODO

前言

本书假定读者具备大学二年级的数学基础，可作为高等院校高年级本科生以及研究生的教材和参考书

• 术语尽可能与自然科学名词审定委员会 1933年公布的《数学名词》中保持一致

单复变量的标准基础教材

• 作者仍然坚信几何方法的基础作用，

复数 complex numbers

复数代数 the algebra of complex numbers

尽量和实数的保持一致

算术运算 Arithmetric Operations

虚数单位imaginary unit i, 有性质$i^2=-1$

通过结合两个实数$\alpha,\beta$，可以构造一个 complex number $\alpha + i \beta$

• pruely imaginary 当$\alpha = 0$
• real 当$\beta= 0$
• Zero 是 唯一的 同时满足上述的
• 相等：实虚部对应相等

封闭的

• 加法$(a+ib)+(c+id)=(a+c)+i(b+d)$
• 乘法$(a+ib)(c+id)=(ac-bd)+i(ad+bc)$
  • 当 非零时，定义除法（勘误，这里中文书开篇就 被除数写错 应该是$\gamma+i\delta$）
  • 这里没有直接用巧妙的 平方差技巧，而是用解方程，的确（解方程需要更少的熟练度）

平方根 Square Roots

给定 $(a+ib)$ 求$(x+iy)^2=(a+ib)$

• 等价于解 $x^2-y^2=a,2xy=b$
  • 推出$x^2+y^2=\sqrt{a^2+b^2}$
  • 从而能计算出
  • $\sqrt{a+ib}=\pm (\sqrt{\frac{a+\sqrt{a^2+b^2}}{2}}+i\frac{\beta}{|\beta|}\sqrt{\frac{-a+\sqrt{a^2+b^2}}{2}})$
  • 这个的意思是说，总能把所有二次根号里的i提出到最外面, 让所有根号内只有实数， 注意上面表达式 根号内都非负实数
• 结论：存在，且两个相反的值
• 零两个根相等
• 正数实平方根
• 负数纯虚平方根

合理性 Justification

还没有研究，所有算术规则保持有效时，方程$x^2+1=0$的解所属的数系的存在性问题

• 回顾实数系R，域：加，乘，结合，交换，分配，0和1分别是加法和乘法的零元（中性元素？neutral elements）
• 中性元素和减法、除法的结果都是唯一的
• 每个域是 整环integral domain， $ab=0$当且仅当$a=0$或$b=0$
• 序， $a<b$当且仅当$b-a \in R^+$
  • 0不是正数
  • 非零数a,那么a,-a一个是正数
  • 两个正数积或和是正数
  • $1=1^2$是正数
  • R包含所有自然数，是域包含所有有理数组成的子域
  • R满足如下的完备性条件，每一个递增并且有界的实数序列都有极限，（见 数学分析原理 的 为什么要定义实数 紧集）
  • 因为$a^2+1$恒正，所以$x^2+1=0$在R中没有解, 现在如果找到一个域F，R是它的一个子域，并且在F中方程$x^2+1=0$有解，记为i，$(x^2+1)=(x+i)(x-i)$, 因此在F中有两个根 i,-i, 令C为F的子集，它的所有$a+ib$的元素组成，差=0时 需要对应相等所以表达式唯一
  • 子集C是F的一个子域，C的构造和F无关（也就是i是根据F来的，而C的定义中有用到这个i) 也就是选取不同的F对应不同的C，而之间会产生同构
  • 定义 复数域 为任意给定的F（F用来定义i）的一个子域C（C要基于实数和i），但还没有证明这样F的存在性，需要构造一个F，包含子域R且F中 (x^2+1=0)有，还是 (a+ib)来构造，只是这里i是纯粹的符号，+也只表示连接，或者用二元组定义（a,b），那么 （a,0）同构于R的子域，类似定义加法乘法，（0，1）满足$x^2+1=0$,
  • 因此它和相应的子域C恒等，证明了复数域的存在，回到简单记法a+bi
• 总的来说 => 随便找个域F，需要引出 i: x^2+1=0的解 同时 包含子域R => 在这个基础上用i 来定义 a+ib 的得到复数系

练习:

• 证明：所有形如$[a,b;-b,a]$的矩阵，矩阵加法，乘法组合起来体系同构于复数系
• $[a,0;0,a]$和实数系同构, $[x,0;0,x]^2+[1,0;0,1]=[0,0;0,0]$的解有一个 取$i=[0,1;-1,0]$, 从而$a[1,0;0,1]+b[0,1;-1,0]$ 就是构造出来的复数系

show that the complex-number system can be thought of as the field of all polynomials with real coefficients module the irreducible polynomial $x^2+1$

• $x^2+1$判别式的确不可约
• 一个是 同态，核，商集的证明
• 另一个是，任何最高幂次 >=2的多项式能在mod以后变为 1次或0次式
  • (f(x)+g(x))mod = ((f mod)+(g mod)) mod
    • 加法抠出 高次的 ，剩余的加法保持且不会变2次，
  • 也是拆分可证 f(x)g(x) mod (x^2+1) = (f mod)(g mod) mod x^2+1
• 这里神奇的是，复数乘法里有减号 (a+ib)(c+id)=(ac-bd)+i(bc+ad)
  • 而 多项式中 $(a+bx)(c+dx)=ac+(bc+ad)x+bdx^2$ 没有减号，
    • 但注意到 $bdx^2 \mod (x^2+1) = bd(x^2+1) - bd = -bd$ 来产生了减号

共轭和绝对值 Conjugation, Absolute Value

实部 Re a, Real

虚部 Im a, Imaginary

推导过程中 $i$和$-i$有相同的性质，因此所有i换成-i，所有规则依然成立

• 复共轭complex conjugation： a+ib <=> a-ib

• 记作$\overline{a+ib}=a-ib$

  • $\overline{\overline{x}}=x$

• $\text{Re} , a=\frac{a+\bar{a}}{2},\text{Im} , a=\frac{a-\bar{a}}{2i}$

• $\overline{a+b}=\bar{a}+\bar{b}$

• $\overline{ab}=\bar{a}\bar{b}$

  • 而这加法乘法性质的证明，从 i 替换成 -i 依然成立的角度来看 立刻得证

• 进一步任何有理运算$R$有 $\overline{R(a,b,c,\cdots)}=R(\bar{a},\bar{b},\bar{c},\cdots)$

• 那么 任何 多项式方程的根x，$\bar{x}$是该方程所有系数取共轭后的新方程的根，特别的如果多项式方程本身是实系数方程，那么说明非实根$x$和$\bar{x}$成对出现

• 勘误，这里 $a\bar{a}=|a|^2, |a| \ge 0$ 恒为正数（中文版错了，写成整数了）或零

• 非负平方根称为 模modulus 或 绝对值absolute value

• 有 $|ab|=|a|\cdot |b|$

  • 乘积的绝对值 = 各绝对值的乘积
  • $|\prod x_i|=\prod |x_i|$
  • 容易扩展到分母非零的除法

• $|a+b|^2=|a|^2+|b|^2+2\text{Re} , a\overline{b}$

• $|a-b|^2=|a|^2+|b|^2-2\text{Re} , a\overline{b}$

• $|a+b|^2 +|a-b|^2 =2(|a|^2+|b|^2)$ 丢到几何里看又是平行四边形对角线

练习:

• 3.$|a|=1$或$|b|=1$ 证明 $|\frac{a-b}{1-\bar{a}b}|=1$ 利用加法和乘法的展开
• 如果$|a|=|b|=1$成立需要什么条件，主要是分母不能=0，也就是$\bar{a}b\neq 1$, 也就是$a\neq b$

4. 什么情况下复未知量 $az+b\bar{z}+c=0$只有一个解

• $ax+bx+c=0,ay-by=0$
• $x=-\frac{c}{a+b},y=0$, 所以$a\neq b,a+b\neq 0$

5. 复数形式拉格朗日等式

• $|\sum_{i=1}^na_ib_i|^2=\sum_{i=1}^n |a_i|^2\sum_{i=1}^n |b_i|^2 -\sum_{1\le i \le j \le n} |a_i\bar{b_j}-a_j\bar{b_i}|^2$
• 对n归纳 + 展开表达式，可证

不等式 Inequalities

首先复数之间没有序的关系，因此所有不等式 的两端都是实数

$-|a| \le \text{Re}, a \le |a|$

$-|a| \le \text{Im}, a \le |a|$

• 从平面上看 固定模长，成立时当且仅当 在四个向的点上
• $|a+b|^2 \le (|a|+|b|)^2$ ,(带入加法展开)
  • $|a+b| \le |a|+|b|$
  • 另一方面 这是三角不等式
  • $|\sum z| \le \sum |z|$ 这个在实数 数学里的重要性（各种邻域，足够近 都是 路径的拼接），它在复数领域同样重要
  • 等号成立条件是平行
• 推论
  • $|a|=|(a-b)+b|\le |a-b|+|b|$
    • $|a|-|b| \le |a-b|$
    • $||a|-|b|| \le |a-b|$
  • 当 复数拆分表示$|a+ib| \le |a|+|b|$
  • 柯西不等式 $|\sum_{i=1}^{n} a_ib_i|^2 \le \sum_{i=1}^n |a_i|^2\sum_{i=1}^n |b_i|^2$
    • 证明$\sum_{i=1}^n |a_i-\lambda \bar{b_i}| = \sum |a_i|^2+|\lambda|^2 \sum |b_i|^2 -2\text{Re}, \bar{\lambda} \sum a_ib_i \ge 0$
    • 取$\lambda=\frac{\sum a_ib_i}{|b_i|^2}$代入
    • 等号成立当且当$a_i,\bar{b_i}$成比例
    • 也可以 归纳法证明柯西不等式

练习

3. $|a_i| < 1, \lambda_i \ge 0, \sum \lambda_i=1$证明$|\sum \lambda_i a_i| < 1$
   1. $|| \le \sum \lambda_i |a_i| < \sum \lambda_i\cdot 1 = 1$, 三角不等式
4. 复数z满足$|z-a|+|z+a|=2|c|$, 证明存在 当且仅当 $|a|\le |c|$
   1. 如果条件成立，求这个情况下的$|z|$的范围
   • 证明，把$v=|c|$除以两边, 再左边用三角不等得到 $\frac{2a}{|c|} \le 2$, 得证
     • 注意到 在复平面上，就是到点$\frac{a}{|c|},-\frac{a}{|c|}$的距离和 = 2，也就是 椭圆，那么椭圆的短轴和长轴$\sqrt{|c|^2-|a|^2}, |c|$

复数的几何表示 the geometric representation of Complex Numbers

用复平面(a,b)表示a+ib

• 需要注意的是，结论应该从性质推导，而不是几何公理，但几何的描述看法会有帮助
• 所以下面很多是“不严密”的，但是有帮助的

几何加法和几何乘法 Geometric Addition and Multiplication

同构保持

• 复数加法 <=> 向量加法
• 零元 <=> 原点
• 数乘 <=> 数乘
• 逆元 <=> 反向向量
• 一个优点 向量的长度 = norm 复数
  • 因此一些 上面不等式定理 就是常见的几何定理了
  • 记作r
• 乘法 需要一点 额外的处理 $(a,b) = (r\cos \theta,r\sin \theta)$
  • 那么复数的乘法 <=> 平面上 $(r_0\cos \theta_0,r_0\sin \theta_0)\times(r_1\cos \theta_1,r_1\sin \theta_1)=((r_0r_1)\cos (\theta_0+\theta_1),(r_0r_1)\sin (\theta_0+\theta_1))$
  • 定义 是 长度相乘，角度相加
    • 证明过程需要一点三角函数的和差化积知识即可
    • 需要注意的是 角度是 mod 2pi的周期的
  • 向量$(1,0)$,$z_0$,$z_1$,$z_0z_1$构成两个相似三角形

练习

2. 证明, 点$a_1,a_2,a_3$当且仅当 $a_1^2+a_2^2+a_3^2=a_1a_2+a_2a_3+a_3a_1$时为等边三角形的三个顶点

   • $(a_1-a_2)^2+(a_2-a_3)^2+(a_3-a_1)^2=0$
   • $x=a_1-a_2,y=a_2-a_3$
   • $x^2+y^2+(x-y)^2=0$
   • $x^2+y^2=xy$
   • $x/y+y/x=1$
   • 如果是等边三角形，那么 这上面是 $1 cos 60°+1 cos(-60°)=1$
   • 但是这个式子 $(t+1/t)cos\theta = 1$的形式，不一定是等边三角形吧???????????

3. 复平面上,三角形顶点$a_1,a_2,a_3$,圆心为

$|o-a_1|=|o-a_2|=|o-a_3|$

$(o-a_1)(\overline{o-a_1})=(o-a_2)(\overline{o-a_2})$

$-\overline{a_1}o-a_1\overline{o}+|a_1|^2=-\overline{a_2}o-a_2\overline{o}+|a_2|^2$

$-\overline{a_1}o-a_1\overline{o}+|a_1|^2=-\overline{a_3}o-a_3\overline{o}+|a_3|^2$

通过$\bar{o}$消除并联立等式

$o=\frac{(|a_1|^2-|a_2|^2)(a_1-a_3)-(|a_1|^2-|a_3|^2)(a_1-a_2)}{(\overline{a_1}-\overline{a_2})(a_1-a_3)-(\overline{a_1}-\overline{a_3})(a_1-a_2)}$

对称化

$o=\frac{|a_1|^2(a_2-a_3)+|a_2|^2(a_3-a_1)+|a_3|^2(a_1-a_2)}{\overline{a_1}(a_2-a_3)+\overline{a_2}(a_3-a_1)+\overline{a_3}(a_1-a_2)}$

二项方程 The Binomial Equation

Moivre’s formula

• $(\cos \theta + i\sin \theta)^n = \cos n\theta + i\sin n\theta$

另一方面 $z^n=r\cos \theta$的一个解是

• $z=\sqrt[n]{r} \cos \frac{\theta}{n}$
• 为了补充剩下 n-1个解, 那么是把$2\pi/n$作为单位 加上去
• 它们 长度相同，幅角均分$2\pi$ 几何上看正好是正n边形的n个顶点
• 其中 右侧=1是重要情况，是均分单位元的情况

解析几何 Analytic Geometry

一个复方程 本来就等价于两个实方程

圆 $|z-a|=r$ , $(z-a)(\bar{z}-\bar{a})=r^2,r\in R,a\in C,z\in C$

复平面直线 $z=a+bt,a\in C,b\in C,t\in R$

• $a_1+b_1t,a_2+b_2t$表示同一条直线 当且仅当$a_2-a_1$和$b_2$都是$b_1$的实数倍数
• 只有$b_1,b_2$成实数倍数时，两个直线平行
• 指向 arg b
• 夹角 $arg b_1/b_2$, 特别的 如果$b_1/b_2$是纯虚数，那么两条直线正交
• $\text{Im}(z-a)/b > 0$可以表示直线a+bt的b方向的逆时针方向的半面（因为 直线视作从a点b方向正向和逆向延伸，而z-a视作从a到z的向量，那么 (z-a)/b 根据几何视角是 向量b向z-a的夹角，那么它的虚数部分的正负可以看作在哪侧）

exercises

show that all circle that pass through $a$ and $1/\bar{a}$ intersect the circle |z|=1 at right angles

• 直接几何证明
• 原点O，a(在圆内)对应A,$1/\bar{a}$对应B，交点C，另一个圆心D
• 显然，O，A，B共线（根据复数运算规则 知道夹角相等）
• 那么 相似三角形有 角OCA=角CBO=角CBA=1/2 角CDA=90-ACD得证

球面表示 The Spherical Representation

引入 无穷，和一些与之有关的四则运算

平面上所有点 连 无穷远点组成 扩充复数平面，

• 约定 每一条直线都经过无穷远点
• 没有 一个半平面包含这个 理想点

单位球面S，三维空间方程 $x_1^2+x_2^2+x_3^2=1$, 除了$(0,0,1)$以外

• 映射一个复数$z=\frac{x_1+ix_2}{1-x_3}$
  • 是一一对应的, how proof ????
  • 专门定义$(0,0,1)$映射到无穷远点
  • 注意到圆 是可以写成 $(x_1+ix_2)(x_1-ix_2)=(1-x_3)(1+x_3)$
• $x_3=\frac{|z|^2-1}{|z|^2+1}$
• $x_1=\frac{z+\bar{z}}{1+|z|^2}$
• $x_2=\frac{z-\bar{z}}{i(1+|z|^2)}$
• 因此可以把球面看成 扩充平面或扩充系数的表示法。
• 注意半球$x_3 < 0$对应圆盘|z|<1, 半球$x_3>0$对应于圆盘的外部$|z|>1$
• 在函数论中S称为 黎曼球面
• 如果 复数平面就是以$x_1$轴，$x_2$轴分别为实轴和虚轴的(x_1,x_2)平面，则变换有简单几何意义，记$z=x+iy$可证 x:y:(-1)=x_1:x_2:(x_3-1)
• 说明点 (x,y,0), (x_1,x_2,x_3),(0,0,1) 在一条直线上。
• 因此 这个对应是以 (0,0,1)为中心的中心投影
• 称为 球极平面投影

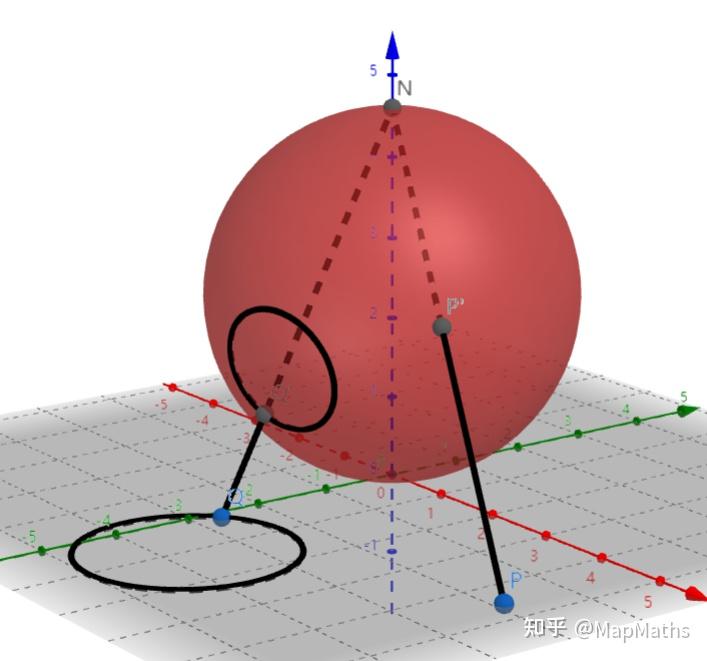
• 对于加法和乘法没有简单解释，方便之处 无穷远点不再特殊
• 更一般的，球上 任意一个圆对应 复平面上 一个圆或一条直线，（哇 直线是半径无穷大的圆

从几何上看，显然球极平面投影将 z 平面上的每一条直线变换为 S 上的一个通过极 (0, 0, 1) 的圆，反之亦然。更一般地，球面上的任一圆对应于 z 平面上的一个圆或一条直线。

平面基础知识:

• 法向量a, $a(x-x_0)=0$ 过点$x_0$垂直法向量的平面

设球上的一个圆所在的平面为 $a_1 x_1 + a_2 x_2 + a_3 x_3 = a_0$，其中，可以

• 假设 $a_1^2 + a_2^2 + a_3^2 = 1$(法向量单位化)
• 且 $0 \leqslant a_0 < 1$。 因为这是上面 $a_0=ax_0$得到的，$x_0$是平面上选点，那么选来从原点到 圆心，正好垂直（和法向量同向）最短，那么小于1
• 用 $z$ 和 $\bar{z}$ 表示时，这个方程有下列形式：

$a_1(z + \bar{z}) - a_2i(z - \bar{z}) + a_3(|z|^2 - 1) = a_0(|z|^2 + 1),$

或

$(a_0 - a_3)(x^2 + y^2) - 2a_1x - 2a_2y + a_0 + a_3 = 0.$

当 $a_0 \neq a_3$ 时，上式是一个圆的方程；而当 $a_0 = a_3$ 时，它表示一条直线。相反，任一圆或直线的方程都可写成这种形式。因此对应是一对一的。

容易算出 $z$ 和 $z’$ 的球极平面投影之间的距离 $d(z, z’)$。如果 $z$ 和 $z’$ 在球面上的点记为 $(x_1, x_2, x_3)$ 和 $(x’_1, x’_2, x’_3)$，则有(球面表达式相加，这里是3维距离不是沿着面的距离)

$(x_1 - x’_1)^2 + (x_2 - x’_2)^2 + (x_3 - x’_3)^2 = 2 - 2(x_1 x’_1 + x_2 x’_2 + x_3 x’_3).$

从(25)和(26)式，经过简单运算后得到

$x_1 x’_1 + x_2 x’_2 + x_3 x’_3 = \frac{(z + \bar{z})(z’ + \bar{z}’) - (z - \bar{z})(z’ - \bar{z}’) + (|z|^2 - 1)(|z’|^2 - 1)}{(1 + |z|^2)(1 + |z’|^2)}$

$= \frac{(1 + |z|^2)(1 + |z’|^2) - 2|z - z’|^2}{(1 + |z|^2)(1 + |z’|^2)}.$

最后得到

$d(z, z’) = \frac{2|z - z’|}{\sqrt{(1 + |z|^2)(1 + |z’|^2)}}.$

当 $z’ = \infty$ 时，上式变为

$d(z, \infty) = \frac{2}{\sqrt{1 + |z|^2}}.$

这个d表示的是，在复平面上两个点，对应到球面的对应点的三维空间中的距离,所以范围也是0到2之间的

练习

1. $z_1,z_2$对应黎曼球面上一个直径的两端点，当且仅当$z_1\bar{z_2}=1$

• 研究 N,O,$z_1,z_2,Z_1,Z_2$共同属于的平面，平面几何容易证明

3. 为一般位置(general position ??)上的正四面体，求各顶点的球极平面投影？？？？？？？？

4. 设$Z_1,Z_2$为球极平面投影$z_1,z_2$, N为北极，证明$NZ_1Z_2$和$Nz_1z_2$相似

• $|Nz_1| |NZ_1| = 1$ 两个都是，所以 $a:b=(1/b):(1/a)$易证

5. 求圆心为a, 半径为R的圆 的球面象的半径

• 考虑NOa这个平面，这个直径端点 映射后还是直径端点，$a-\frac{a}{|a|}R,a+\frac{a}{|a|}R$这两个点的映射, 带入d的表达式

TODO

中文数是 1.1.1 这样的序号，英文没有 章节号，而作为其它书的阅读感来说, 好像 章节.序号更舒服?

这本书 一个小节都有直接习题，而不是章节总的习题

https://web.ma.utexas.edu/users/demason/Ahlfors%20Exercises.pdf