Stanford Machine Learning 科普
图片主要来源于官方的讲义PDF以及Wikipedia
监督学习
线性回归
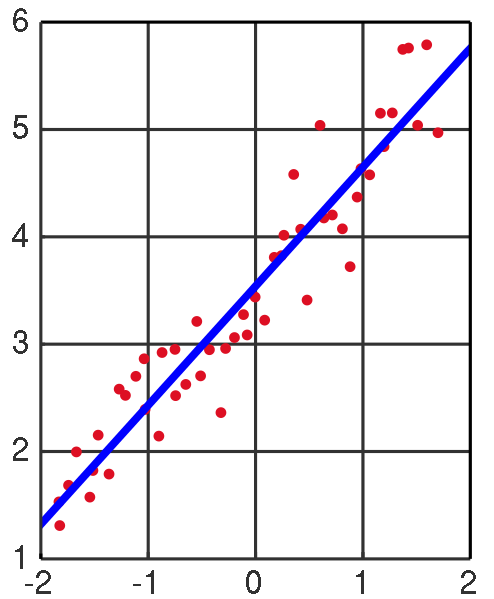
将输入数据,如图中的红点,求得一条直线表示数据中的线性关系,并且这条直线在概率期望上达到最佳(后面算法省略这句)。
梯度下降
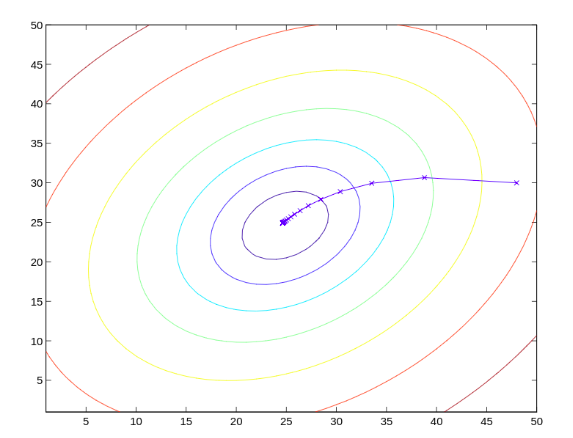
找函数极值小值点,图中相同颜色线为等高线,越靠近中心高度越低,运用高数的梯度运算和梯度下降能够得到如图中蓝色x标记的逐步逼近的极值点。
Normal Equation
同样是解决线性回归问题,和梯度下降不同的是,运用矩阵运算,直接得到参数的表达式
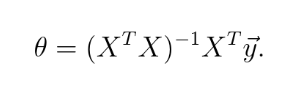
Logistics 回归
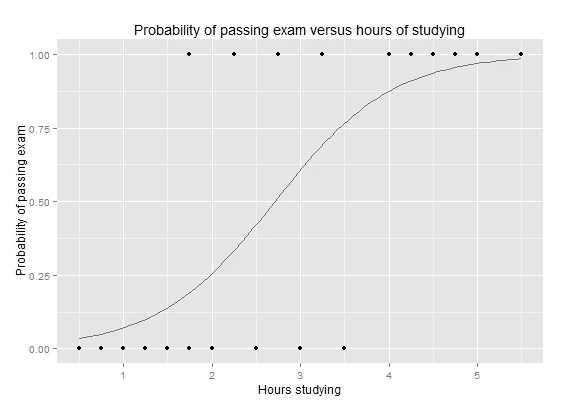
分类算法,对一侧数据0,另一侧数据1的训练数据建立分类器,图中的点是 训练输入,线是得到的logistics函数
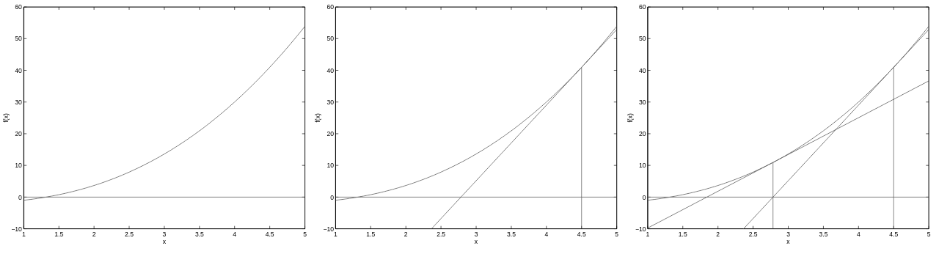
高斯切线法
高数知识,二次收敛,加速点的收敛,如图 通过计算切线与坐标轴的交点作为下一次的迭代起始值。
广义线性模型GLM
按照所提出的假设模型,能够直接得到所需要的 拟合函数,可以用来证明上面 的线性回归中最小二乘法是最优,以及Logistics 回归中的函数选取。

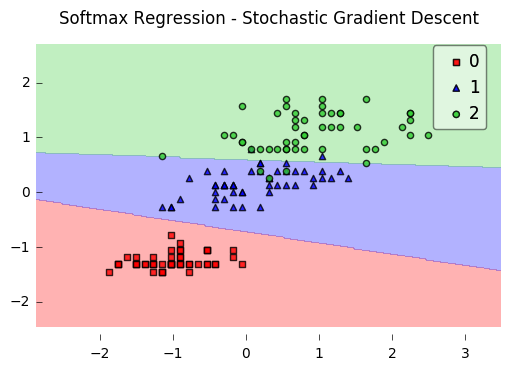
softmax 回归
分类到对互斥的k个类别,公式推导采用带入GLM
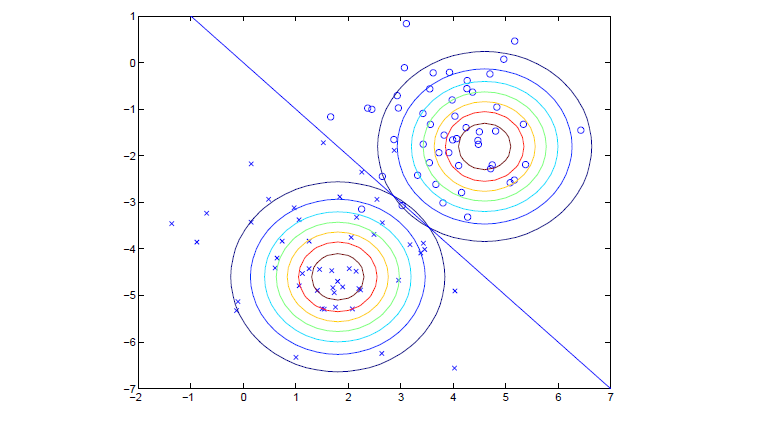
高斯判别分析GDA
对0分布满足高斯分布,1分布也满足高斯分布的分布进行线性分类。
朴素贝叶斯
整体与特征来判断整体的分类,如垃圾邮件根据出现的词汇进行分类,很暴力直接计算概率
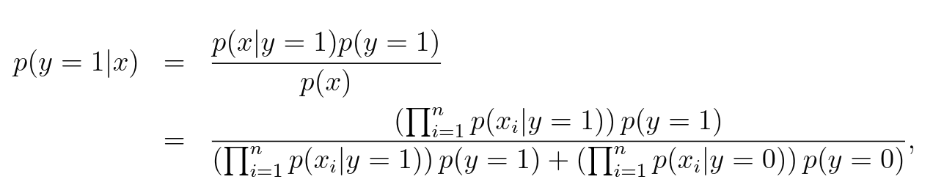
拉普拉斯平滑
解决朴素贝叶斯中可能出现的0除以0的情况,分子+1,分母+可分的种类数k
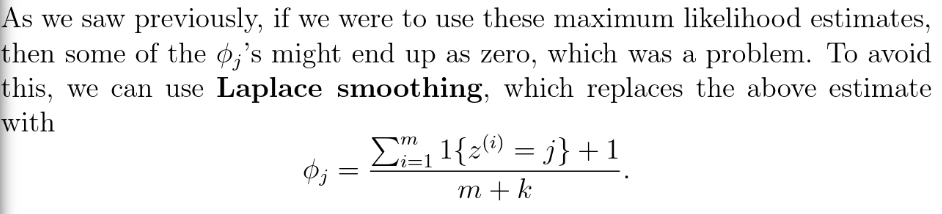
最优线性分类器
如图能够找到将 数据分开,并且离分割线最近的点的距离值最大的分类器。
拉格朗日对偶、KKT
用于具体解决 最优线性分类器的支撑方法

核函数
将变量非线性变化映射到高维空间,减小计算量,表示量,配合其它算法使用能获得高维空间性质。

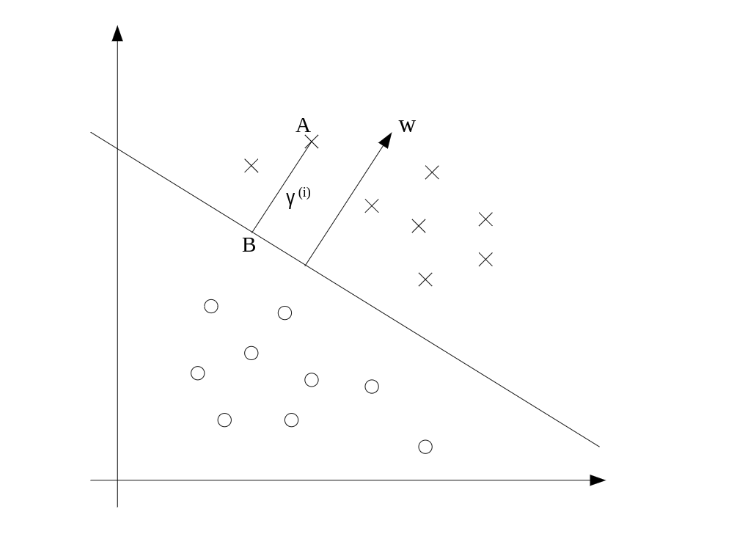
支持向量机SVM
将低维不可线性分割的 通过核函数映射到高维度,再在高维中进行最优线性分割
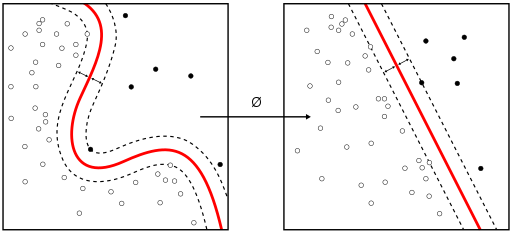
L1 Regularization
在有部分异常点时的分割,通过添加惩罚项解决如下图异常点导致变化过大的问题。

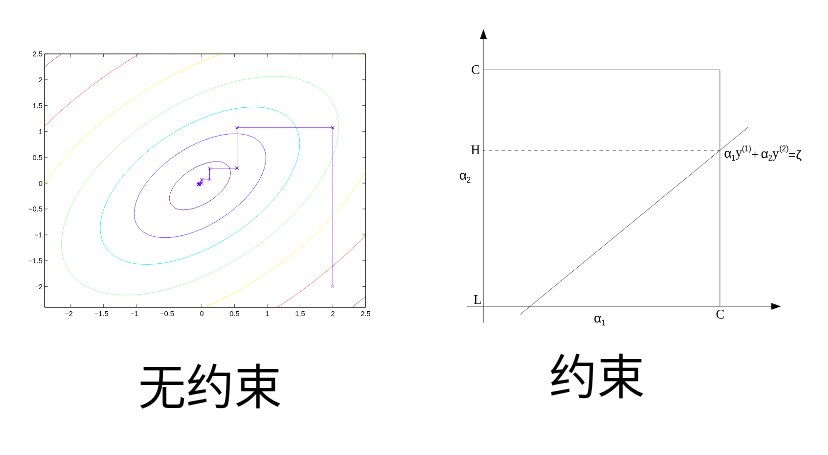
SMO
对于多个参数 每次选一个参数进行取极值点,SMO能在带等式与不等式的约束限定情况下,每次两个参数逐步逼近。
均方误差MSE
能够用于分析 过拟合 还是 欠拟合

错误分析
按步骤替代/隔离分析,逐个增加或逐个减少。按训练误差 方差,实验 误差方差分析。
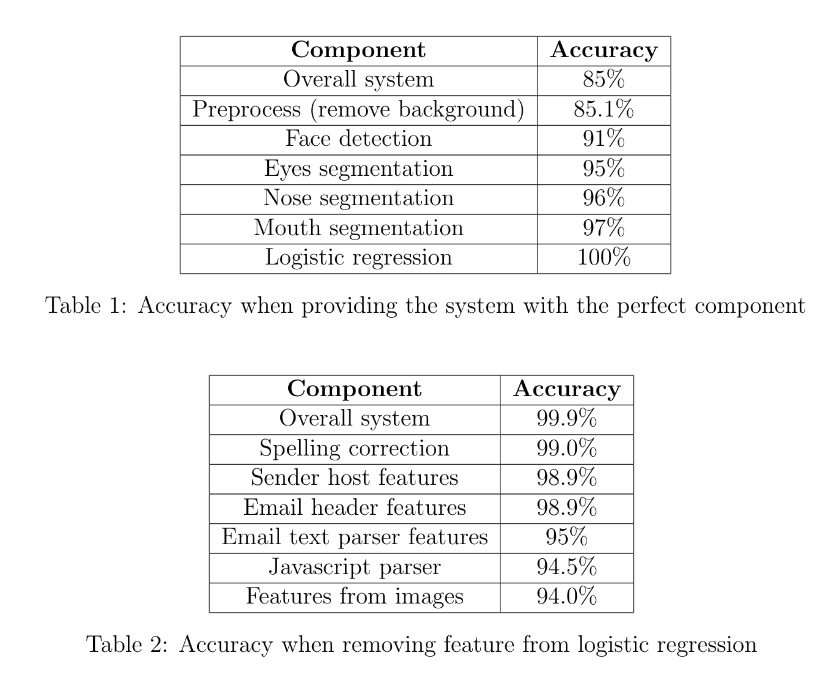
VC维、hoeffding不定式
用于证明概率下训练集和误差的上下界存在性。
验证方式、模型选择
将部分的训练数据不用于训练而用于检验模型
感知器
感知器:转换后的值小于0输出-1,大于等于0输出
无监督学习
k-means
对无标记的点进行分类(寻找分类的中心)
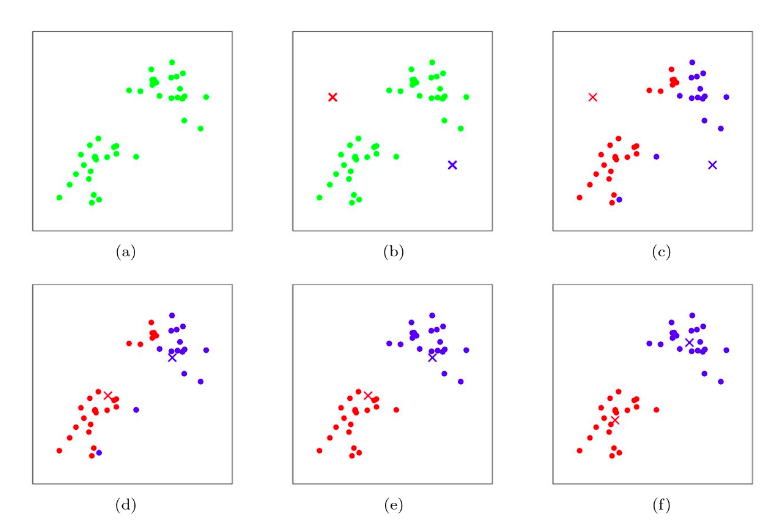
高斯混合模型GMM
可以看作类似前面的高斯判别模型GDA,但是现在的输入数据是无标记的
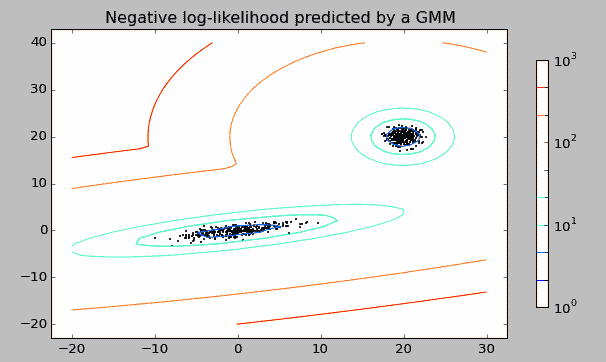
EM算法
用于GMM等无标记的混合模型的分离,先假设隐含变量Z以及它的分布Q,和k-means的思想类似,E-step优化Q,M-step优化参数,重复直到收敛 [使用Jensen不等式],分离效果见上图
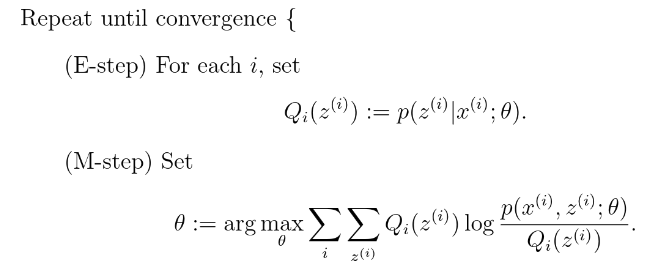
因子分析
对训练集量少,维数大,分类的类别少的分布进行分类,思想是建立隐含低维度变量z,通过矩阵转化投影到高维,再加上高斯扰动误差
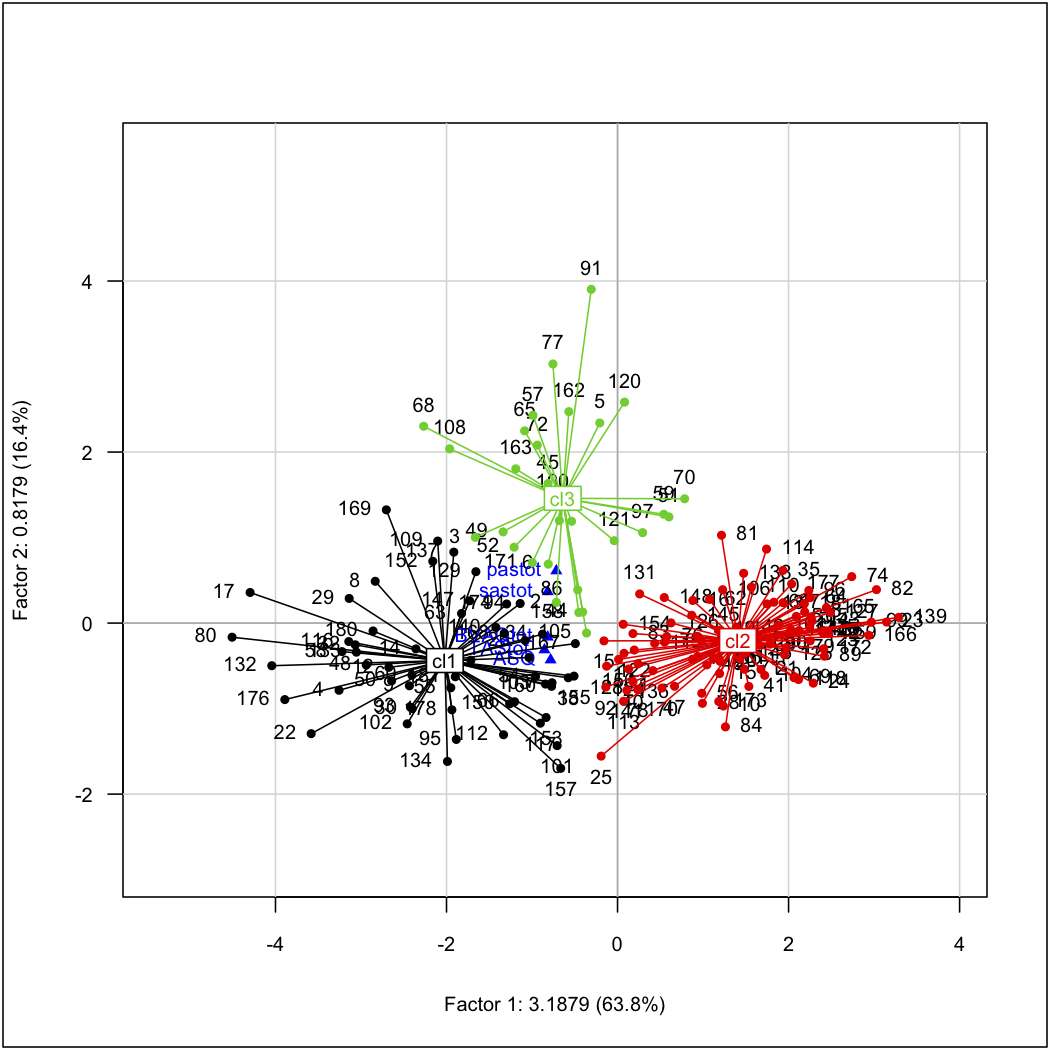
主成分分析PCA
对于高维空间的数据,找到其前k个相互正交的关键维度的向量,可用线性代数奇异值分解SVD进行快速计算。可以用于降维度,作为其它算法的预处理步骤,或找到关系的主要方面。
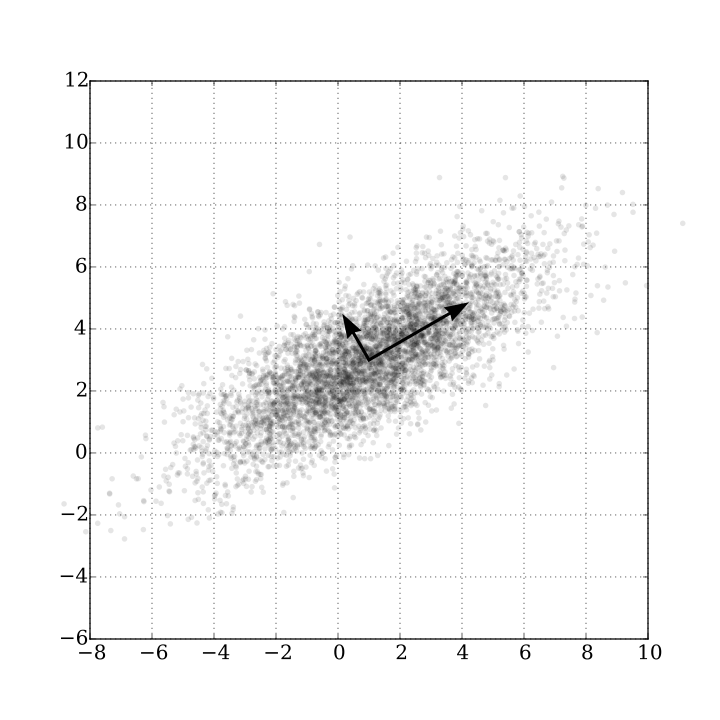
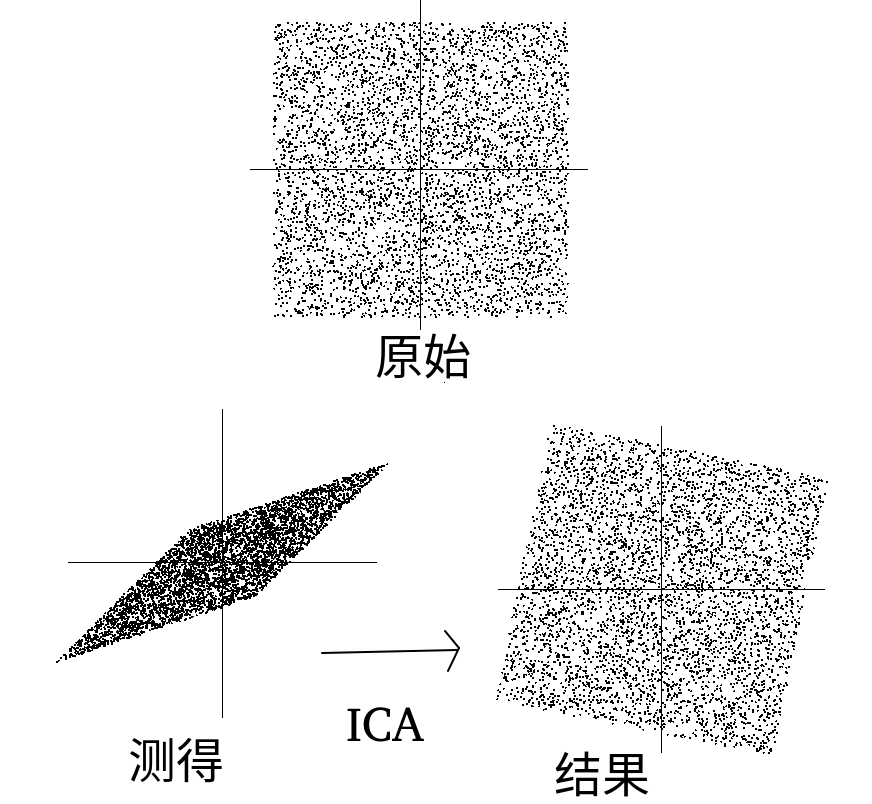
独立成分分析ICA
对于多维度,相互独立的非高斯分布成分,找到每个成分的轴,并将所有轴转换为正交轴。可用于特征提取,特征分离,如音频分离,计算人脸识别面部特征向量,对脑电波数据分离预处理去除眨眼和心跳信号。
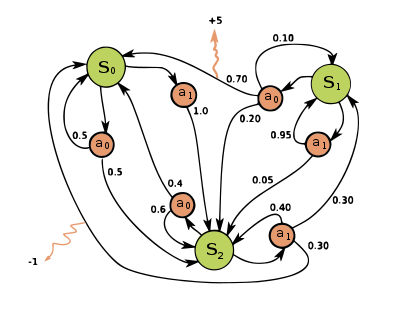
马尔科夫模型
马尔科夫决策过程 MDP
能够学习带有状态,和基于状态动作的一类事情,学出一个策略集,如自动驾驶,需要设置奖励函数,概率函数等参数函数。策略迭代和值迭代
离散化连续状态的MDP
也就是字面意思离散化,在2维下工作一般不错,高维度后无论是维数灾难还是离散化难度,以及模型最终产物都难以普遍满意
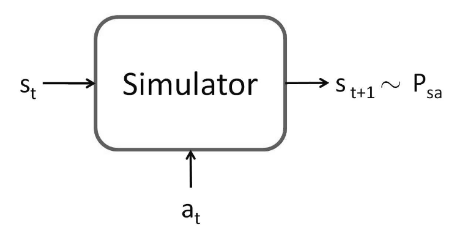
MDP中的模型模拟器
用于概率状态未知时,用实验+拟合得到模型,从而代替概率函数的位置
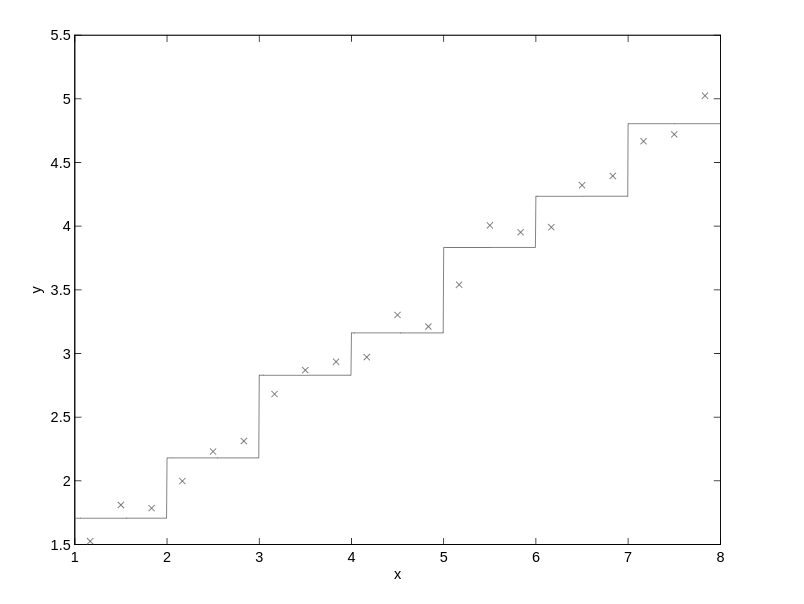
线性二次型调节控制LQR
解决状态依赖于前一个状态前一个动作以及时间的策略选择,在有限时间内用动规(倒着递推),多次实验线性拟合基于时间的。对于非线性函数仅能取较近的输入值,用近似的切线做近似的线性处理。通过加强奖励函数,初始值(时间T)矩阵,等限定。得出结论,动作与状态的线性相关,且计算过程中可以省去无关迭代

kalman滤波
将观测值转化为概率上的真实值
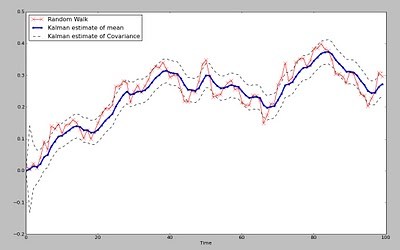
LQG
LQG=LQR+kalman滤波
微分动规DDP
根据当前决策选定轨迹,做LQR,更新决策,重复。从函数上理解是函数逐步靠近,即使是一个不那么好的模拟器

pegasus策略搜索
处理非线性模型函数的情况。选取随机序列并重复使用于模型训练,在模型选择时选取非线性的模型(如logistics 函数),用极大似然去找该模型下的最优策略。
