解pell方程
就过程进行书写,去掉自己尝试思考的中间步骤,只留下有效的过程
初版文章
原题目
https://projecteuler.net/problem=66
$d = 1\to 1000$,d是非平方数
对于每个$d$ 求最小的正整数$x$使得$x^2-dy^2=1$,其中$x$,$y$都是正整数,
最后对所有这些$x$求最大的$x$
本文针对给定的$d$讨论具体的方程解法
读懂本文你可能需要的前置知识
抽屉原理
二元一次方程
绝对值
有理数/无理数
模运算
矩阵运算
数列/递推数列
二项式展开
反证法
归纳法
不等式(缩放,三角不等式)
共轭实数(不太知道怎么翻译比较好,还是对偶实数? 描述的就是$a+b\sqrt{m}$与$a-b\sqrt{m}$
题解
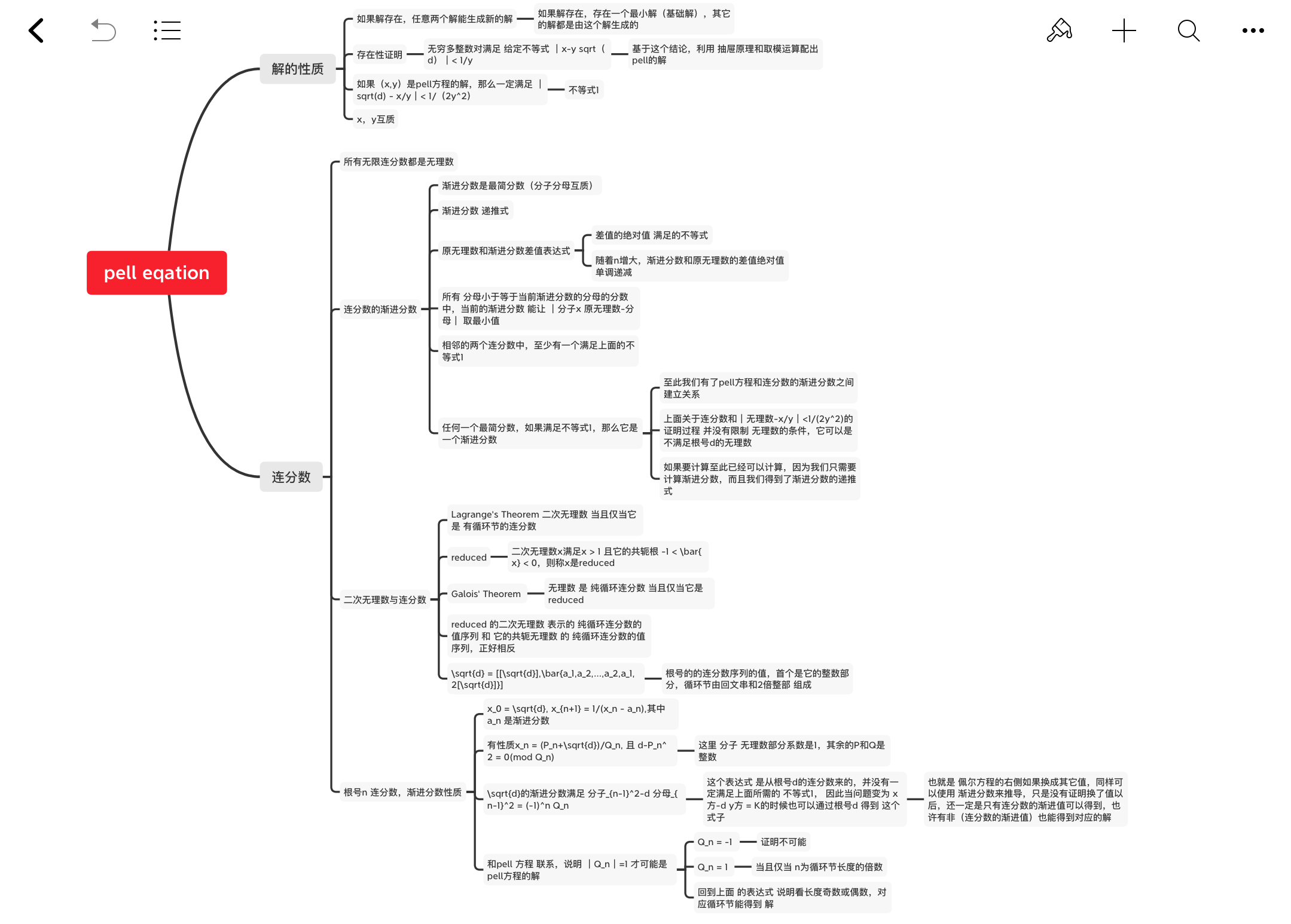
![2020 12 05 pe 066]()
pell方程的解
解的存在性证明
对于给定$d$,存在无穷多对整数$(x,y)$满足 $|x-y\sqrt{d}|<\frac 1y$
取任意正整数$q_0 > 1$
把区间$[0,1)$均分为$q_0$个左闭右开的区间,则每部分长度为$\frac 1{q_0}$, 考虑 $t \sqrt{d}$的小数部分($t = 0,\cdots,q_0$ 共计$q_0+1$个),抽屉原理,必定有两个落在同一区间, 即存在$0\leq i < j\leq q_0$使得 $| \{i \sqrt{d}\} - \{j \sqrt{d}\} | <\frac 1{q_0}$
即$|x-(j-i)\sqrt{d}| = | \{i \sqrt{d}\} - \{ j \sqrt{d}\} | < \frac 1{q_0} \leq \frac 1{j - i}$, 其中$x$用于去掉整数部分
这里要注意的是知道$i < j$,和它们的小数部分落在同一个区间,所以这里应该是它们的小数部分相减的绝对值,而不是相减的绝对值的小数部分,例如q取2, 一个取0.4,一个1.3,它们都在[0,0.5)的区间里,但是如果$|1.3-0.4|$ 再取绝对值的小数部分,得到的是0.9而不是0.1,对于x来说,只要增减1就能在最终的值上切换成功.
得到一个解$(x,y=j-i)$
取$\frac 1{q_1} < |x-(j-i)\sqrt{d}|$
如下这样, 相同的$(x,y)$一定是等于关系, 因此如下这样可以产生无限多的解
$|x_3-y_3\sqrt{d}| <\frac 1{q_3} < |x_2-y_2 \sqrt{d}| < \frac 1{q_2} < |x_1-y_1\sqrt{d}| <\frac 1{q_1} < |x_0-y_0 \sqrt{d}| < \frac 1{q_0} < 1$
反复使用抽屉原理, 证明存在性, 并配出一个解
对于上一个结论中的无限多个解
$0 < \left|x^2-dy^2\right| $
$=\left|x+y\sqrt{d}\right|\cdot\left|x-y\sqrt{d}\right|$
$=\left|x-y\sqrt{d}+2y\sqrt{d}\right|\cdot\left|x-y\sqrt{d}\right| $
$\le (\left|x-y\sqrt{d}\right|+\left|2y\sqrt{d}\right|)\cdot\left|x-y\sqrt{d}\right| $
$< \left(2y\sqrt{d}+\frac{1}{y}\right)\cdot\frac{1}{y}$
$\le 2\sqrt{d}+\frac 1{y^2} $
$\le 2 \sqrt{d} + 1 $
说明这无限多个$(x,y)$的取值,对$|x^2-dy^2|$的计算结果是有限范围内的整数
如果你看下面我提供的youtube链接,你会发现证明的细节步骤会有些差别,视频里,并没有这么精细的放缩,因为最终目的只需要证明有限个取值,而在中间直接放缩到 $\le |3y\sqrt{d}|$
抽屉原理,存在正整数$k$, 使得$|x^2-dy^2|=k$ 的 解有无限个
考虑这些解$(x \bmod k,y \bmod k)$ , 结果的方案数$\leq k^2$,也是有限的,
抽屉原理,存在$(M_x,M_y)$,有无限个$i$ 满足 $(x_i \bmod k, y_i \bmod k) = (M_x,M_y)$,在这无限组中取两组$(x_1,y_1),(x_2,y_2)$
令 $X=|\frac{x_1x_2-y_1y_2d}{k}|,Y=|\frac{x_2y_1-x_1y_2}{k}|$
有 $X^2-d \cdot Y^2 = \frac{(x_1^2-d \cdot y_1^2)(x_2^2-d \cdot y_2^2)}{k^2} = 1$
因为 $(x_2y_1-x_1y_2)\bmod k = (x_1y_1-x_1y_1) \bmod k = 0 \bmod k = 0$,所以$Y$是非负整数
注意到 $x^2-dy^2$ 的取值范围为 $\pm k$ (2个,有限个),但可取的$(x,y)$有无限对,抽屉原理,因此存在$(x_i,y_i)\neq(x_j,y_j)$使得 $x_i^2-dy_i^2=x_j^2-dy_j^2$ 这时 $\frac{x_i}{y_i} \neq \frac{x_j}{y_j}$ (否则代入前式子得到$x_i=x_j$), 即$Y$为非$0$正整数
因为$X$是有理数且满足pell方程,所以它是整数, 且$X = \sqrt{1+dY^2} \neq 0$
综上, 一定存在解
注,上面X,Y的等式看着很突兀,但在看了Youtube视频之后意识到了, 既然 基础解的幂次能有效,且证明了负幂次也有效,那么 $ x^2-dy^2 = 1 = k/k = \frac{x_1^2-dy_1^2}{x_2^2-dy_2^2}$ 然后通分化简就有了上面那个显得突兀的令
解的性质(基础解)
如果解存在 $x,y \ge 0$
任意两个解能生成新的解
若$(x_0,y_0),(x_1,y_1)$ 是 $x^2-d y^2=1$ 的解
$1 = (x_0^2-d y_0^2)(x_1^2-d y_1^2)$
$= (x_0 + \sqrt{d} y_0)(x_0 - \sqrt{d} y_0)(x_1 + \sqrt{d} y_1)(x_1 - \sqrt{d} y_1)$
$= (x_0 + \sqrt{d} y_0)(x_1 + \sqrt{d} y_1)(x_0 - \sqrt{d} y_0)(x_1 - \sqrt{d} y_1)$
$= (x_0x_1 + dy_0 y_1 + \sqrt{d} (y_0x_1+y_1 x_0))(x_0x_1 + dy_0 y_1 - \sqrt{d} (y_0x_1+y_1x_0))$
$= (x_0x_1 + dy_0 y_1)^2 - d(y_0x_1+y_1 x_0)^2$
那么$(x_0x_1 + dy_0y_1, y_0x_1+y_1x_0)$也是一个解
如果定义 $A(x,y) = x+\sqrt{d}y,x > 0,y > 0$ 为一个解, 那么有 $A(x_0x_1 + dy_0 y_1,y_0x_1+y_1 x_0) = A(x_0,y_0)\cdot A(x_1,y_1)$
存在一个基础解(最小解),所有解都是由基础解生成的
下面证明所有解都是最小解生成的
反证法, 因为$y$越大$x$越大, 设$(x_1,y_1)$为最小解, $(x_k,y_k)$不是由最小解,通过上述乘积的幂次方法生成的一个解
根据$y$越大$x$越大的性质,存在一个整数$n$
$(x_1+y_1 \sqrt{d})^n < (x_k+y_k \sqrt{d}) < (x_1+y_1 \sqrt{d})^{n+1} $, 同时乘$(x_1-y_1 \sqrt{d})^n$有
$1 < (x_k+y_k \sqrt{d}) (x_1-y_1 \sqrt{d})^n < (x_1+y_1 \sqrt{d}) $
注意到中间的表达式 也是一个解(且因为 它 大于1, 所以它的共轭 在0到1之间, 而它和它的共轭 只有 y的符号不同, 所以它的x和y的符号均为正)
这与最小解定义矛盾,所以所有解都是最小解生成的
pell方程性质小结
关于pell方程的解 ,现在有了两个结论
- 一定存在解
- 有最小的基础解, 所有解都是由它的幂次得到的, $(1,0)$ 正好看作它的$0$次方的结果
下面开始看看连分数。
连分数
定义
形如
$\alpha = a_0 + \cfrac{1}{a_1 + \cfrac{1}{a_2 + \cfrac{1}{a_3 + \cfrac{1}{\ddots,}}}} $
例如
$ \sqrt{2} = 1 + \cfrac{1}{2 + \cfrac{1}{2 + \cfrac{1}{2 + \cfrac{1}{2 + \cfrac{1}{2 + \cfrac{1}{2 + \ddots}}}}}} $
展开的剩余部分是在[0,1)之间
所有无限连分数都是无理数
证明:如果一个数是有理数,把它写成分数的形式,再按照连分数的方式展开,你会发现这过程就是辗转相除,分子分母单调递减 所以一定有限,它的逆否命题就是要证明的性质
渐进分数(分子,分母等性质)
分子$h_n$分母$k_n$
递推式
渐进分数,把上述表示无理数$\alpha$的连分数部分截断所得到的分数
若$h,k$分别为渐进分数的分子和分母,根据简化为分数的过程
$\begin{bmatrix} h_n & k_n \end{bmatrix} = \begin{bmatrix} 1 & 0 \end{bmatrix} \cdot \begin{bmatrix} a_n & 1 \\ 1 & 0 \end{bmatrix} \cdot \begin{bmatrix} a_{n-1} & 1 \\ 1 & 0 \end{bmatrix} \cdots \begin{bmatrix} a_0 & 1 \\ 1 & 0 \end{bmatrix} $
然而这不好建立递推关系,稍做变形
$\begin{bmatrix} h_n & k_n \\ ? & ? \end{bmatrix} = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \cdot \begin{bmatrix} a_n & 1 \\ 1 & 0 \end{bmatrix} \cdot \begin{bmatrix} a_{n-1} & 1 \\ 1 & 0 \end{bmatrix} \cdots \begin{bmatrix} a_0 & 1 \\ 1 & 0 \end{bmatrix} $
$\begin{bmatrix} h_n & k_n \\ ? & ? \end{bmatrix} = \begin{bmatrix} a_n & 1 \\ 1 & 0 \end{bmatrix} \cdot \begin{bmatrix} a_{n-1} & 1 \\ 1 & 0 \end{bmatrix} \cdots \begin{bmatrix} a_0 & 1 \\ 1 & 0 \end{bmatrix} $
$\begin{bmatrix} h_n & k_n \\ ? & ? \end{bmatrix} = \begin{bmatrix} a_n & 1 \\ 1 & 0 \end{bmatrix} \cdot \begin{bmatrix} h_{n-1} & k_{n-1} \\ ? & ? \end{bmatrix} $
左式的底部可以确定
$\begin{bmatrix} h_n & k_n \\ h_{n-1} & k_{n-1} \end{bmatrix} = \begin{bmatrix} a_n & 1 \\ 1 & 0 \end{bmatrix} \cdot \begin{bmatrix} h_{n-1} & k_{n-1} \\ ? & ? \end{bmatrix} $
又因为递推关系,右边式子相当于左式带入n-1
$\begin{bmatrix} h_n & k_n \\ h_{n-1} & k_{n-1} \end{bmatrix} = \begin{bmatrix} a_n & 1 \\ 1 & 0 \end{bmatrix} \cdot \begin{bmatrix} h_{n-1} & k_{n-1} \\ h_{n-2} & k_{n-2} \end{bmatrix} $
综上
$h_n = a_n \cdot h_{n-1} + h_{n-2}$
$k_n = a_n \cdot k_{n-1} + k_{n-2}$
渐进值 $\frac{h_n}{k_n} = \frac{a_n \cdot h_{n-1} + h_{n-2}}{a_n \cdot k_{n-1} + k_{n-2}}$
且根据计算过程,可知 $h_n,k_n$互质
等式
由上面的递推关系再递推有
$k_nh_{n-1}-k_{n-1}h_n=-(k_{n-1}h_{n-2}-k_{n-2}h_{n-1})=(-1)^n $,
$k_nh_{n-2}-k_{n-2}h_n=a_n(k_{n-1}h_{n-2}-k_{n-2}h_{n-1})=a_n(-1)^{n-1} $,
设无理数$\alpha$ 的精确表示为$[a_0,a_1,\cdots,a_n,x_{n+1}]$,即是最后$a_{n+1}$替换为精确的非整数值$x_{n+1}$,有$1\leq a_{n+1}<x_{n+1}<a_{n+1}+1,(n>=1)$
与原无理数的距离 $\alpha - \frac{h_n}{k_n}$
表达式
根据上方计算渐进值得到的公式,同理递推式有
$\alpha =\frac{x_{n+1}h_n+h_{n-1}}{x_{n+1}k_n+k_{n-1}} $
$\alpha - \frac{h_n}{k_n} =\frac{x_{n+1}h_n+h_{n-1}}{x_{n+1}k_n+k_{n-1}} -\frac{h_n}{k_n} $
$=\frac{h_{n-1}k_{n}-h_nk_{n-1}}{k_n(x_{n+1}k_n+k_{n-1})}$
$=\frac{(-1)^n}{k_n(x_{n+1}k_n+k_{n-1})}$
$|\alpha -\frac{h_n}{k_n}| =\frac{1}{k_n(x_{n+1}k_n+k_{n-1})} < \frac{1}{k_n(a_{n+1}k_n+k_{n-1})} = \frac{1}{k_nk_{n+1}}$
注意到$k_n$的递推式,容易发现它是单调递增的正整数,所以渐进分数真的是趋近($n$趋于无限大, 渐进分数与原无理数距离趋近于0)
单调递减
$|k_n\alpha - h_n|$单调递减
证明:
$|k_n\alpha - h_n| - |k_{n-1}\alpha - h_{n-1}|$
$ = |k_n(\alpha - \frac{h_n}{k_n})| - |k_{n-1}(\alpha - \frac{h_{n-1}}{k_{n-1}})|$
$ = \frac 1{x_{n+1}k_n+k_{n-1}} - \frac 1{x_{n}k_{n-1}+k_{n-2}} $
$ = \frac {(x_{n}k_{n-1}+k_{n-2})-(x_{n+1}k_n+k_{n-1})}{(x_{n+1}k_n+k_{n-1})(x_{n}k_{n-1}+k_{n-2})}$
$ = \frac {((a_n+\frac 1{x_{n+1}})k_{n-1}+k_{n-2})-(x_{n+1}k_n+k_{n-1})}{(x_{n+1}k_n+k_{n-1})(x_{n}k_{n-1}+k_{n-2})}$
$ = \frac {(x_{n+1}(a_nk_{n-1}+k_{n-2})+k_{n-1})-x_{n+1}(x_{n+1}k_n+k_{n-1})}{x_{n+1}(x_{n+1}k_n+k_{n-1})(x_{n}k_{n-1}+k_{n-2})}$
$ = \frac {(x_{n+1}k_n+k_{n-1})-x_{n+1}(x_{n+1}k_n+k_{n-1})}{x_{n+1}(x_{n+1}k_n+k_{n-1})(x_{n}k_{n-1}+k_{n-2})}$
$ = \frac {(1-x_{n+1})(x_{n+1}k_n+k_{n-1})}{x_{n+1}(x_{n+1}k_n+k_{n-1})(x_{n}k_{n-1}+k_{n-2})} < 0$
由此也可知和原无理数的距离$|\alpha - \frac{h_n}{k_n}|$单调递减
$|\alpha - \frac{h_n}{k_n}|-|\alpha -\frac{h_{n-1}}{k_{n-1}}|$
$=\frac {|{k_n}\alpha-{h_n}|-\frac {k_n}{k_{n-1}}|{k_{n-1}}\alpha-{h_{n-1}}|}{k_n}$ (因为$k_n$单调递增
$<\frac {|{k_n}\alpha-{h_n}|-|{k_{n-1}}\alpha-{h_{n-1}}|}{k_n} < 0$
最优接近 $|\alpha - \frac{h}{k}|$与$|k\alpha - h|$
https://proofwiki.org/wiki/Convergents_are_Best_Approximations
和渐进数同分母的所有分数中,渐进数最接近原无理数
若$(h_n,k_n)$是一个渐进分数,则对于分母$k_n$,分子取$h_n$时,整个分数最接近原无理数
取任意$h\neq h_n$,根据三角不等式
$|\alpha -\frac{h}{k_n}| \geq |\frac{h-h_n}{k_n}| - |\alpha - \frac{h_n}{k_n}|$
$>\frac 1{k_n} - \frac 1{k_nk_{n+1}} $,因为n足够大 $k_{n+1}>=3$有
$> \frac 1{k_n} - \frac 1{2k_n} $
$=\frac 1{2k_n} $
$> \frac 1{k_nk_{n+1}} > |\alpha -\frac{h_n}{k_n}|$
证明了$h_n$是最接近的分子
即 $|k_n\alpha - h|$在 $h=h_n$时取最小值
$0 < k \le k_n$的所有分数$\frac{h}{k}$中, 渐进数$\frac{h_n}{k_n}$能使$|k\alpha - h|$为最小值, $(h_{n-1},k_{n-1})$ 使它为次小值
考虑任意$(h,k),(0 < k < k_n)$,且$\frac hk$的为最简分数, 且不是渐进数
若它不是最简分数, 则它是它最简分数的t倍, 比它最简分数得到的值更大
因为已经证明了渐进数随着$n$增大, $|k_n\alpha - h_n|$单调递减,且渐进数分子分母互质,所以如果是渐进数则对应渐进数的该表达式 更大
设二元一次方程组
$h_nx+h_{n-1}y=h$
$k_nx+k_{n-1}y=k$
则有$(x,y)=(\frac {hk_{n-1}-kh_{n-1}}{h_nk_{n-1}-h_{n-1}k_n},\frac {hk_{n}-kh_{n}}{h_nk_{n-1}-h_{n-1}k_n}) = ((-1)^{n-1}(hk_{n-1}-kh_{n-1}),(-1)^{n-1}(hk_{n}-kh_{n}))$
因为$\frac hk$不是渐进分数,所以$x,y$都是非零整数,又因为$k < k_n$和$k_nx+k_{n-1}y=k$有:$x,y$异号
因为$\alpha - \frac {h_n}{k_n} =\frac{(-1)^n}{k_n(x_{n+1}k_n+k_{n-1})}$的分子为$(-1)^n$,分母为正数,
所以$\alpha - \frac {h_n}{k_n}$和$\alpha - \frac {h_{n-1}}{k_{n-1}}$异号
即$k_n\alpha - {h_n}$和$k_{n-1}\alpha - {h_{n-1}}$异号
有$x(k_n\alpha - {h_n})$和$y(k_{n-1}\alpha - {h_{n-1}})$同号
$|k\alpha -h| = |(k_nx+k_{n-1}y)\alpha - (h_nx+h_{n-1}y)|$
$= |x(k_n\alpha - {h_n}) + y(k_{n-1}\alpha - {h_{n-1}})|$,因为同号
$= |x(k_n\alpha - {h_n})|+|y(k_{n-1}\alpha - {h_{n-1}})|$,因为$x,y$非零整数:
$|k\alpha - h| > |k_n\alpha - {h_n}|$且$|k\alpha -h|>|k_{n-1}\alpha - {h_{n-1}}|$, 得证
$|\alpha - \frac hk|<\frac 1{2k^2}$(pell方程必要的不等式, 渐进数判定不等式)
https://proofwiki.org/wiki/Condition_for_Rational_to_be_a_Convergent
连续的两个渐进数中至少有一个满足该不等式
反证法, 证明:
假设都不满足,有
$0 \leq |\alpha-\frac{h_{n+1}}{k_{n+1}}| - \frac{1}{2k_{n+1}^2} + |\alpha-\frac{h_{n}}{k_{n}}|-\frac{1}{2k_{n}^2}$, 因为$\alpha - \frac{h_{n}}{k_{n}} =\frac{(-1)^n}{k_n(x_{n+1}k_n+k_{n-1})}$正负交替,所以
$ = |\frac{h_{n+1}}{k_{n+1}}-\frac{h_{n}}{k_{n}}|-\frac 1{2k_{n+1}^2} -\frac 1{2k_{n}^2}$
$ = |\frac{h_{n+1}k_{n}-h_{n}k_{n+1}}{k_{n+1}k_{n}}|-\frac 1{2k_{n+1}^2} -\frac 1{2k_{n}^2}$
$ = \frac 1{k_nk_{n+1}} -\frac 1{2k_{n+1}^2} -\frac 1{2k_{n}^2}$
$ = \frac {-(k_n-k_{n+1})^2}{2k_{n}^2k_{n+1}^2} < 0$
矛盾, 因此至少有一个满足, 得证
任何最简分数如果满足该不等式,那么它是一个渐进分数
证明
设$\frac hk$满足不等式$|\alpha - \frac hk|<\frac 1{2k^2}$,则存在$n$使得渐进数分母满足 $k_{n+1} > k \ge k_n $, 若$\frac hk \neq \frac{h_n}{k_n}$,即$k_n < k$
$0 \leq \frac{|hk_n-h_nk|-1}{kk_n}$
$= |\frac{h}{k}-\frac{h_n}{k_n}|-\frac{1}{kk_n}$,因为三角不等式,有
$\leq |\alpha -\frac{h}{k}|+|\alpha -\frac{h_n}{k_n}|-\frac{1}{kk_n}$, 因为假设满足的不等式
$< \frac 1{2k^2} + \frac 1{k_n}|k_n\alpha - h_n|-\frac{1}{kk_n}$,因为上面的最优接近, 所有$< k_{n+1}$ 的分母中 都大于 $(h_n,k_n)$的方案
$< \frac 1{2k^2} + \frac 1{k_n}|k\alpha - h|-\frac{1}{kk_n}$
$= \frac 1{2k^2} + \frac {k}{k_n}|\alpha - \frac hk|-\frac{1}{kk_n}$因为假设满足的不等式
$< \frac 1{2k^2} + \frac {k}{k_n}\cdot \frac 1{2k^2}-\frac{1}{kk_n}$
$= \frac {k_n-k}{2k^2k_n} < 0$
矛盾,因此$\frac hk$和某个渐进数相等
注记:最开始该文的版本,的渐进分数的部分直接使用的是pell方程中$\sqrt{d}$,其中$d$是非平方正整数,但为了写project euler 100需要的证明,需要把它扩充到实数(当然也是成立的),所以这部分改写了一次
Lagrange’s Theorem 二次无理数与有循环节的连分数
quadratic irrational(二次无理数) 定义: 二次整式多项式的根 $\frac{-b\pm \sqrt{b^2-4ac}}{2a}$ 或者形如$\frac{P+\sqrt{D}}{Q}$
一个无理数是二次无理数, 当且仅当它的连分数是循环连分数: An irrational number is quadratic irrational if and only if its continued fraction is periodic.
循环连分数一定是二次无理数
按照连分数的写法,令循环节的值为$t$
还原为分数,有$x=\frac{a t + b}{c t +d},t = \frac{et+f}{gt+h}$ 变换左表达式用$x$表示$t$,带入右侧表达式得到$\frac{ix+j}{kx+l} = \frac{mx+n}{ox+p}$,其中字母$a \to p$均为整数,且注意到$x$为无理数, 所以化简后一定是二次方程
二次无理数一定是循环连分数
定义,对于无理数x
$f(x) = x-1 (x>1)$
$f(x) = \frac{1}{\frac{1}{x}-1} , (x<1)$
对应到连分数展开$[a_0,a_1,a_2,\cdots]$,即是将首个数字减少$1$,($x>1$时就是$a_0$减去$1$,$x<1$时就是$a_1$减去$1$)
令$x_1=x,x_{n+1}=f(x_n)$,可以知道 这是一个无限数列
如果$x$满足$ax^2+bx+c=0$,写作$x \in g(a,b,c)$
那么$x-1$ 满足$a(x-1)^2+(2a+b)(x-1)+(a+b+c) = ax^2+bx+c=0$, 即$x-1 \in g(a,2a+b,a+b+c)$
那么$\frac{1}{\frac{1}{x}-1} = \frac{x}{1-x}$ 满足$(a+b+c)(\frac{x}{1-x})^2+(b+2c)\frac{x}{1-x}+c = \frac{ax^2+bx+c}{(1-x)^2} = 0$, 即$\frac{1}{\frac{1}{x}-1} \in g(a+b+c,b+2c,c)$
所以$f(x)$满足 $f(x)\in g(a,2a+b,a+b+c)$ 或 $f(x)\in g(a+b+c,b+2c,c)$
不失一般性,写作$x_n \in g(s_n,t_n,u_n)$,有 $s_n > 0$, 否则把三元组同时换号
注意到上式 $(2a+b)^2-4a(a+b+c)=b^2-4ac=(b+2c)^2-4(a+b+c)c$
说明了 $t_n^2-4s_nu_n$是和$n$无关的值
反证法: 如果只有有限个$u<0$,那么从某一处开始,$s>0,u>0$且$t<0$(因为 $x > 0$)
那么意味着 $t$ 严格单调递增,(因为$t$的变化关系是$t=2s+t$或$t=t+2u$),整数是离散的,矛盾
所以有无限个$u_n<0$, 即无限多$s_n u_n < 0$
注意到 $t_n^2-4s_nu_n$是常数,抽屉原理, 至少有一个三元组$[s_n,t_n,u_n]$ 出现了三次以上,一个二次方程有两个解,所以有满足的$x_n=x_m,m>n$
得证 连分数展开有循环
Theorem 1. If x is a positive quadratic irrational then its continued fraction is eventually periodic.
Galois’ Theorem 纯循环连分数与reduced二次无理数
https://proofwiki.org/wiki/Definition:Quadratic_Irrational/Reduced
Definition 1.24. $x$ 是二次方程的一个根,$\overline{x}$ 是另一个根,那么如果 $x > 1$ 且 $-1 < \overline{x} < 0$.那么称 x 为 reduced
Theorem 1.25. (Galois’ Theorem) 无理数a. a是纯循环连分数(从$a_0$开始的循环节),当且仅当 x is reduced. If $x = [\overline{a_0, a_1, a_2, . . . , a_{l−1}}]$ and $\overline{x}$ 是它共轭实数, then $-\frac{1}{x} = [\overline{a_{l−1}, . . . , a_2, a_1}].$
reduced二次无理数 是 纯循环连分数
设reduced二次无理数$x$的一个渐进分数为$[a_0,a_1,\cdots,a_n], x>1,-1<\overline{x}<0$
那么有 $x_{n+1}=\frac{1}{x_n-a_n}$ 表示 按照展开从n处向后取值
$\overline{x_{n+1}} = \frac{1}{\overline{x_n-a_n}} = \frac{1}{\overline{x_n}-a_n}$,(因为 两个形如$A+B\sqrt{C}$的无理数相乘为有理数,说明相乘后的无理数的系数为0,所以更改其中一个无理数的系数的正负,另一个无理数系数的正负更改即可)
注意到$x \ge 1$有$a_0 \ge 1$,所以 $a_n \ge 1$
下面归纳证明 $-1 < \overline{x_n} < 0 $
若 $-1 < \overline{x_n} < 0$
有 $\frac{1}{\overline{x_{n+1}}} = \overline{x_n} - a_n < -1$
即 $-1 < \overline{x_{n+1}} < 0$,得证
$-1 < \overline{x_n} = \frac{1}{\overline{x_{n+1}}}+a_n < 0$
$ 1 > -\frac{1}{\overline{x_{n+1}}}-a_n > 0$
$ a_n = [ -\frac{1}{\overline{x_{n+1}}} ] $ ($a_n$等于分式的整数部分)
因为上面已经证明 如果是二次无理数,那么必定有循环节,所以存在$x_i = x_j,(i < j )$
即$\overline{x_i}=\overline{x_j}$
即$a_{i-1}=[-\frac{1}{\overline{x_i}}]=[-\frac{1}{\overline{x_j}}] = a_{j-1}$
即$x_{i-1}=a_{i-1}+\frac{1}{x_i} = a_{j-1}+\frac{1}{x_j} = x_{j-1}$, 意义就是如果两个后缀相等,那么它们各向前一个 也相等,综上逐步迭代$a_0 =a_{j-i}$
因此证明了 如果一个二次无理数是 reduced,那么它是个纯循环连分数
纯循环连分数 是 reduced二次无理数
首先有循环节的连分数一定是二次无理数(上面证过了)
因为是纯循环,所以$a_0 \ge 1$,所以$a_n \ge 1$,有$x > 1$
假设周期为$n$, 有 $x_n = x = [\overline{a_0,a_1,\cdots,a_{n-1}}]$
根据上面推过的递推式 $x = \frac{x_nh_{n-1}+h_{n-2}}{x_nk_{n-1}+k_{n-2}} = \frac{xh_{n-1}+h_{n-2}}{xk_{n-1}+k_{n-2}}$
化简 $k_{n-1}x^2+(k_{n-2}-h_{n-1})x-h_{n-2}=0$
下面证明这个方程除了$x$ (已经有 $x>1$了)的另一个根$\overline{x}$满足$-1 < \overline{x} < 0$
连续函数零点存在性定理
$x = 0$时 原式子 $=-h_{n-2} < 0$
$x = 1$时 原式子
$= k_{n-1}+(h_{n-1}-k_{n-2})-h_{n-2}$
$= (a_{n-1}k_{n-2}+k_{n-3}) + (a_{n-1}h_{n-2}+h_{n-3}) -k_{n-2}-h_{n-2}$
$= (a_{n-1}-1)(h_{n-2}+k_{n-2}) + (h_{n-3}+k_{n-3}) $
$ > 0 $
说明了另一个根$-1 < \overline{x} < 0$
至此证明了 reduced 和 纯循环之间的 充要
reduced二次无理数 纯循环连分数的 原无理数与它的共轭相反倒数的连分数数值关系
若 $x = [\overline{a_0, a_1, a_2, . . . , a_{l−1}}]$ 且 $\overline{x}$ 是它共轭实数, 有 $-\frac{1}{\overline{x}} = [\overline{a_{l−1}, . . . , a_2, a_1,a_0}].$
考虑有限的连分数 $x = [a_0,a_1,\cdots,,a_n], y=[a_n,a_{n-1},\cdots,a_0] , a_i > 0$
$h_n,k_n$为$x$的分子分母,$h_n’,k_n’$为$y$的分子分母
要证明 $\frac{h_n}{h_{n-1}} = \frac{h_n’}{k_n’}$ 且 $\frac{k_n}{k_{n-1}} = \frac{h_{n-1}’}{k_{n-1}’}, n \ge 1$ 且分子分母对应相等(因为是最简分数,所以只要证明了分数相等就有对应相等了)
注意到上面 $h_n = a_n \cdot h_{n-1} + h_{n-2}$,同时除以 $h_{n-1}$
$\frac{h_n}{h_{n-1}} = a_n + \frac{1}{\frac{h_{n-1}}{h_{n-2}}}$
递归展开 可以得到 $\frac{h_n}{h_{n-1}} = [a_n,a_{n-1},\cdots,a_0]$,
注意到 $k_n = a_n \cdot k_{n-1} + k_{n-2}$,同理 $\frac{k_n}{k_{n-1}} = [a_n,a_{n-1},\cdots,a_1] $(注意是$a_1$不是$a_0$)
根据上面的递归展开的结论 和 y的分子分母定义 有
$\frac{h_{n}}{h_{n-1}} = [a_{n},a_{n-1},\cdots,a_0] = \frac{h_{n}’}{k_{n}’}$
$\frac{k_{n}}{k_{n-1}} = [a_{n},a_{n-1},\cdots,a_1] = \frac{h_{n-1}’}{k_{n-1}’}$
且分子分母对应相等(因为是最简分数)
若$x$是纯循环连分数,则$x$为reduced 二次无理数,则$-\frac{1}{\overline{x}}$为reduced的二次无理数,则$-\frac{1}{\overline{x}}$为纯循环连分数
假设直接取$n+1 = $ 两个循环节长度的最小公倍数
$k_{n}x^2+(k_{n-1}-h_{n})x-h_{n-1}=0$
令
$y = [\overline{a_n,a_{n-1},\cdots,a_0}] = [a_n,a_{n-1},\cdots,a_0,y]$
$y = \frac{h_n’y+h_{n-1}’}{k_n’y+k_{n-1}’}$
上面证明了对应相等$h_n=h_n’,k_{n-1}=k_{n-1}’, h_{n-1}=k_{n}’,h_{n-1}’=k_n$
做对应替换,$y = \frac{h_ny+k_{n}}{h_{n-1}y+k_{n-1}}$
展开 $k_{n}{(-\frac{1}{y})}^2+(k_{n-1}-h_{n})(-\frac{1}{y})-h_{n-1}=0$
$-\frac{1}{y} = \overline{x}$ 得证($y$为正 所以 不可能等于$x$)
至此 Theorem 1.25. (Galois’ Theorem) 无理数a. a是纯循环连分数(从a0开始的循环节),当且仅当 x is reduced. If $x = [\overline{a_0, a_1, a_2, . . . , a_{l−1}}]$ and $\overline{x}$ 是它共轭实数, then $-\frac{1}{\overline{x}} = [\overline{a_{l−1}, . . . , a_1, a_0}].$ 得证
$\sqrt{d}$ 的 连分数$ = [\lfloor \sqrt{d} \rfloor,\overline{a_1,a_2,\cdots,a_2,a_1,2\lfloor \sqrt{d} \rfloor}]$
Theorem 1.26 $d$是非平方数,那么$\sqrt{d} = [\lfloor \sqrt{d} \rfloor,\overline{a_1,a_2,\cdots,a_2,a_1,2\lfloor \sqrt{d} \rfloor}]$
也就是 是从第二位开始循环节,且循环节最后一个是它的整部的2倍,且剩余部分是回文
令$x=\lfloor \sqrt{d} \rfloor + \sqrt{d}$ 则$\overline{x} = \lfloor \sqrt{d} \rfloor - \sqrt{d}$
注意它们的取值范围发现$x$是reduced 二次无理数
因此 $ x = \lfloor \sqrt{d} \rfloor + \sqrt{d} = [\overline{2\lfloor \sqrt{d} \rfloor,a_1,a_2,\cdots,a_{l-1}}]$
$ = [2\lfloor \sqrt{d} \rfloor,\overline{a_1,a_2,\cdots,a_{l-1},2\lfloor \sqrt{d} \rfloor}]$
$ \sqrt{d}= [\lfloor \sqrt{d} \rfloor,\overline{a_1,a_2,\cdots,a_{l-1},2\lfloor \sqrt{d} \rfloor}]$
根据Galois’ Theorem有
$\frac{1}{\sqrt{d}-\lfloor \sqrt{d} \rfloor} = -\frac{1}{\overline{x}} = [\overline{a_{l-1},\cdots,a_2,a_1,2\lfloor \sqrt{d} \rfloor}]$
也就是$\sqrt{d} = [\lfloor \sqrt{d} \rfloor,\frac{1}{\sqrt{d}-\lfloor \sqrt{d} \rfloor}]$
$ = [\lfloor \sqrt{d} \rfloor,\overline{a_{l-1},\cdots,a_2,a_1,2\lfloor \sqrt{d} \rfloor}]$
因此 循环内容 和 回文性质 得证
利用连分数 解 Pell’s Equation
因为平方带来的对称性,只考虑$x>0,y>0$的解
$x=\sqrt{d}$的后缀连分数 可以表示为 $x_n=\frac{P_n+\sqrt{d}}{Q_n}$
若$d$为非平方数,$x=\sqrt{d}$,
则对于任意$n$,存在整数$P_n,Q_n$满足$x_n=\frac{P_n+\sqrt{d}}{Q_n}$和$d-P_n^2 = 0 \pmod{Q_n}$
当$n=0$时$(P_0,Q_0) = (0,1)$满足,归纳法,若$n$时能满足上述两点性质,则
$x_{n+1} = \frac{1}{x_n-a_n}$
$=\frac{1}{\frac{P_n+\sqrt{d}}{Q_n}-a_n}$
$=\frac{Q_n}{P_n+\sqrt{d}-a_n{Q_n}}$ (通过分母有理化)
$=\frac{Q_n(P_n-a_nQ_n-\sqrt{d})}{(P_n-a_nQ_n)^2-d}$
$=\frac{a_nQ_n-P_n+\sqrt{d}}{\frac{d-(P_n-a_nQ_n)^2}{Q_n}}$
$(P_{n+1},Q_{n+1}) = (a_nQ_n-P_n,\frac{d-(P_n-a_nQ_n)^2}{Q_n})$
现在要证明的就是 它是满足$\frac{P_{n+1}+\sqrt{d}}{Q_{n+1}}$的形式,并且满足上面的取模
也就是要证明$Q_{n+1}$是整数
$Q_{n+1} = \frac{d-P_n^2}{Q_n}+2a_nP_n-a_n^2Q_n$, 因为$n$时有 $d-P_n^2 = 0 \pmod{Q_n}$所以 $Q_{n+1}$是整数
又因为$Q_nQ_{n+1}=d-P_{n+1}^2$ 所以 $d-P_{n+1}^2 = 0 \pmod{Q_{n+1}}$ 得证
$\sqrt{d}$的渐进分数满足 $h_{n-1}^2-d k_{n-1}^2=(-1)^n Q_n$
对于$n \ge 2$ 要证明 $h_{n-1}^2-d k_{n-1}^2=(-1)^n Q_n$
证明:
$\sqrt{d} = \frac{x_n h_{n-1}+h_{n-2}}{x_nk_{n-1}+k_{n-2}}$
把$ x_n = \frac{P_n+\sqrt{d}}{Q_n}$带入并通分化简
$(P_nk_{n-1}+Q_nk_{n-2}-h_{n-1})\sqrt{d} = P_nh_{n-1}+h_{n-2}Q_n-k_{n-1}d$, 无理数 = 有理数, 只有都为$0$
即 $P_nk_{n-1}+Q_nk_{n-2}=h_{n-1}$ 且 $P_nh_{n-1}+h_{n-2}Q_n=k_{n-1}d$
所以有 $h_{n-1}^2-dk_{n-1}^2 = h_{n-1}(P_nk_{n-1}+Q_nk_{n-2})-k_{n-1}(P_nh_{n-1}+h_{n-2}Q_n)$
$= Q_n(h_{n-1}k_{n-2}-h_{n-2}k_{n-1})$
$= (-1)^nQ_n$
pell方程的解一定是$\sqrt{d}$的渐进分数
若$(x,y)$是 pell方程$x^2-dy^2=1$的解$(d>1,x>y>0)$,则
$|\sqrt{d} - \frac{x}{y}| = |\frac{dy^2-x^2}{y^2(\sqrt{d}+\frac{x}{y})}| < \frac{1}{2y^2}$ (从一定程度上说明了 为什么前面要去证明 小于$\frac{1}{2y^2}$)
根据前面的结论, 知道满足这个表达式的一定是 无理数$\sqrt{d}$ 的 渐进数, (但渐进数不一定是解)
(Yang.pdf那个paper下面的部分蛮多笔误的 不过能看懂证明思路)
因为上面有 $h_{n-1}^2-dk_{n-1}^2=(-1)^nQ_n$ 也就是如果要满足pell方程 那么$|Q_n|=1$,分类讨论$Q_n$
假设 $\sqrt{d}$的 最小周期长度为l
分类讨论 $Q = -1$
$Q_n \neq -1, n > 0$
证明
注意到上面根据$\sqrt{d}$的表达式 证明了$n>0$时,$x_n$是纯循环连分数,也就是reduced 二次无理数
如果$Q_n = -1$ 因为$x_n=\frac{P_n+\sqrt{d}}{Q_n}$,所以有 $x_n=-P_n-\sqrt{d} > 1$,有$-1<-P_n+\sqrt{d} < 0$ (Galois)
但$\sqrt{d} < P_n < -\sqrt{d} - 1$,矛盾 所以$Q_n \neq -1$, 对于$Q_0 = 1$也不为$-1$,得证
分类讨论 $Q = 1$
$Q_n = 1$当且仅当$n$为循环节长度的倍数才有
证明
若于$n>1$若$Q_n=1$那么有$x_n=P_n+\sqrt{d}$,它的共轭 $-1 < P_n-\sqrt{d} < 0$ 即 $P_n=\lfloor \sqrt{d} \rfloor$所以 $x_n = \lfloor \sqrt{d} \rfloor + \sqrt{d}$
$ \lfloor \sqrt{d} \rfloor +\sqrt{d} = x_n = 2\lfloor\sqrt{d}\rfloor + \frac{1}{\frac{1}{\sqrt{d} - \lfloor \sqrt{d} \rfloor}} $ 即 $ x_{n+1} = \frac{1}{\sqrt{d} - \lfloor \sqrt{d} \rfloor}$
$ \sqrt{d} = x_0 = \lfloor \sqrt{d} \rfloor + \frac{1}{\frac{1}{\sqrt{d} - \lfloor \sqrt{d} \rfloor}}$ 即 $x_1 = \frac{1}{\sqrt{d} - \lfloor \sqrt{d} \rfloor}$
说明了 它的下一个数$x_{n+1} $和$x_1$相等, 这说明如果$Q_n = 1$ 那么n是当且仅当循环节长度的倍数(如果为1则循环节长度)
循环节长度 与 pell方程的最小解
最后回到这里 $h_{n-1}^2-dk_{n-1}^2=(-1)^nQ_n = (-1)^n $ 也就是再看个奇偶,最后得到了pell方程和连分数比较紧密的结论
假设 $\sqrt{d}$的 最小周期长度为$l$
那么对应pell 方程的最小解
$(x,y) = {h_{l-1},k_{l-1}}$ 长度为偶数
$(x,y) = {h_{2l-1},k_{2l-1}}$ 长度为奇数
回顾历程
- pell方程解一定存在
- pell方程所有解为基础解的幂次
- 连分数分子 分母 递推式
- 连分数,分子分母相关性质(分子分母互质性,原无理数与渐进数差值表达式,差值绝对值单调递减性,连分数是最给定分母以及更小分母中最接近原无理数,任何满足 渐进数充分不等式 的数字是渐进数(这个不等式是pell方程 的必要条件))
- Lagrange’s Theorem : 二次无理数 与 有循环节的连分数 等价关系
- Galois’ Theorem : reduced二次无理数 与 纯循环连分数 等价关系
- $x = \sqrt{d} = [\lfloor \sqrt{d} \rfloor,\overline{a_1,a_2,\cdots,a_2,a_1,2\lfloor \sqrt{d} \rfloor}] $, 以及连分数性质(精确的$x_n = \frac{P_n+\sqrt{d}}{Q_n}$表示 和 渐进数性质$h_{n-1}^2-dk_{n-1}^2=(-1)^nQ_n$)
- 分类讨论$Q_n = 1 , -1$与$n$的取值, 循环节长度, 与最后的结论
方法涉及
- 反复抽屉原理,绝对值,无理数,模运算
- 二项式展开,不等式,唯一最小(有术语吗),无理数,反证法
- 矩阵乘法,归纳法/递推关系
- 归纳法/递推,互质,不等式放缩,三角不等式,反证法,二元一次方程组,巧妙正负值+不等式。 很多方法都是多次
- 归纳,反证,单调+整数离散+有限,二次函数
- 共轭实数,反向推,归纳法
- 归纳法,上面的分子分母等式性质
- -1的幂次,分类讨论,Lagrange,Galois
然后还有很多整数的离散性质
参考
Continued fraction
Pell equation
Yang.pdf
stanford crypto pell
millersville periodic-continued-fractions
下面这个youtube非常推荐,他讲得很系统,并不是证明了就好,而是按照了每步都能抽象出结论的推导过程,然后和连分数相关的没讲,主要在讲pell 方程的解的性质
YouTube:Number Theory:Pell’s Equation part 1
A short proof and generalization of Lagrange’s theorem on continued fractions
purely periodic continued fractions
总结&感受
有些结论在证明过程中其实是缩小了范围,有些结论其实放大定义域之类也是成立的,但在证明过程中却只使用了所需要的部分。这类的从定义域和对应的要证明的逻辑不是“完美对应”的,但是足够,不知道是好还是不好。
证明的结论之间引用过程,感觉画成网状或者树状关系图会更好?
看youtube了上的讲解视频,会发现有一种写代码的抽取函数感觉,和我上面完全拆开证明不一样,抽函数的感觉其实在数学里大概是叫做“令”+“引理”,感觉和完全展开比较,的确能减少很多心智负担啊!如果你也能打开youtube建议去看看
另外比如有些 强结论要用的时候,即使你证出了相对弱的结论,但没有证明出强结论,其实相当于“没有用”,比如上面 基础解,的平方,的n次方,和任意另一组解能产生新的解的证明。当然如果能证明出,那些就是过程了,但不是步骤(虽然我上面有写进文中,因为要简洁整理的话,直接强结论证明,即可其它的弱的可以直接省略
虽然视频看的时候的确感觉到老师和同学的口算不如国内,但自从自己思考过十进制的意义以后,感觉数值计算都不再重要,有的是计算机,不需要人类来算。
youtuber james cook 有证明一个 同系数二元二次方程 之间的关系,可以用它来 从 不是解的东西里生成解(感觉好像不是特别行,因为一个等式的 四个值仅仅由两个变量控制而不是3个?)!(Quadradic Forms) Q(u+v)+Q(u-v)=2(Q(u)+Q(v)),然后以此建立树,考虑其中的“正负交替路线”river
多核没智力还是搞不动数学啊,
这篇文章整理了很多篇其它资料,所以在符号使用上还不够统一,之后看有空整理一下
在我快写完这一篇文章的时候发现了 一个超理论坛-连分数入门 注册需要一点点水平XD,这篇是带着例子讲解写的!(大自看了一下 感觉很棒 推荐), 又 有些性质证明方式不止一种,例如我本篇文章所抄来的证明 二次无理数和有循环节的充要 会感觉更漂亮一些
有些paper写到后面还是很多笔误,不过看通了也是能理解具体过程
有一个想法是 哪些结论是关键或者说证明的难点,其实可以这样想,现在,把文章中一些部分换成填空,你还能不能补全整个文章,不需要完全一样,只要能证明就行。这样想的话,就会知道所谓的难点是在哪。