Codeforces Round 493 (Div. 1)

發表於 更新於 分類於 ， Disqus： 文章字數： 1.3k 所需閱讀時間 ≈ 4 分鐘
容斥(493D1C,497D1B)

493D1C

输入

给你n*n(1<=n<=1'000'000)的格子

要求

每个格子 图上 有3种颜色可以选择，

如果所有格子都上完色后， 存在一列或一行的颜色全部相同，则称作lucky

输出

求 所有lucky的方案数 modulo 998244353

解法

翻译自官方

A{i}表示 有i 行 颜色相同
B{i}表示 有i 列 颜色相同

然后直接 容斥原理公式(搜索一下就能找到的公式) 计算 $A_1 \cup A_2 \ldots A_n \cup B_1 \cup B_2 \ldots B_n$

然后因为 这些行列在哪里和我们的计算无关，所以对于A{i}可以看成选i行，让这i行每行内颜色相同，也就是C(n,i)倍的 方案数

所以有那个公式$ans = \sum_{i=0 \ldots n, j=0 \ldots n, i + j > 0} C_n^i C_n^j (-1)^{i + j + 1} f(i, j)]$

f(i,j)表示前i行j列 lucky的方案数

然后 具体表示f(i,j)

i,j其中一个有0的情况，这种情况，以行举例来说，同色的行 之间是可以不同色的，所以是$3^k$

$f(k, 0) = f(0, k) = 3^k \cdot 3^{n (n - k)}$

其它情况，这样的话 因为 如果至少有1行+1列是同色的，那么所有的同色的行列 都是同色的，这样就是3

$f(i, j) = 3 \cdot 3^{(n - i)(n - j)}$

很明显 这个n，肯定不是能做出来的

那么 分两块，ij带0的 O(n)时间内算出

其它部分 看数学操作了,首先 带入f(i,j)

$ans=\sum_{i=1}^{n}\sum_{j=1}^{n}C_n^iC_n^j(-1)^{i+j+1}3\cdot3^{(n-i)(n-j)}$

换元 $i \to n-i, j \to n - j$

$ans = 3 \sum_{i=0}^{n - 1}\sum_{j = 0}^{n - 1} C_n^{n - i} C_n^{n - j} (-1)^{n - i + n - j + 1} \cdot 3^{ij}$

等价化简

$ans = 3 \sum_{i=0}^{n - 1} \sum_{j = 0}^{n - 1} C_n^i C_n^j (-1)^{i + j + 1} \cdot 3^{ij}$

分离

$ans = 3 \sum_{i=0}^{n - 1} C_n^i (-1)^{i+1} \sum_{j = 0}^{n - 1} C_n^j (-1)^{j} \cdot (3^i)^j$

乘法分配率

$ans = 3 \sum_{i=0}^{n - 1} C_n^i (-1)^{i+1} \sum_{j = 0}^{n - 1} C_n^j (- 3^i)^j$

考虑对后面的求和简化，考虑下面式子

$(a + b)^n = \sum_{i = 0}^{n} C_n^i a^i b^{n - i}$

这里 我们把a取1，b取$-3^i$，再注意到求和到n不是n-1，进行一个加减消除，最后可以把ans化简为

$ans = 3 \sum_{i=0}^{n - 1} C_n^i (-1)^{i+1} [(1 + (-3^i))^n - (-3^i)^n]$

这个式子，可以累加求和在O(n)时间内做出了

众所周知的 模逆元 快速幂 取模什么的就不说了

感觉这里分类是我的问题，我自己想 始终把三个颜色分开想怎么计算，这里合在一起了。

497D1B

输入

t个询问(1<=t<=100'000)

每个询问A,B,C (1<=A,B,C<=100'000)

要求

若a是A的因子，b是B的因子，c是C的因子，则(a,b,c)记为1种方案

(a,b,c),(a,c,b),(b,a,c),(b,c,a),(c,a,b),(c,b,a)视作同一种方案

输出

求总方案数

解法

看了别人超级宽的代码后 才看懂解法，虽然我第一眼也知道是个容斥

首先众所周知，预处理每个数的因子个数。

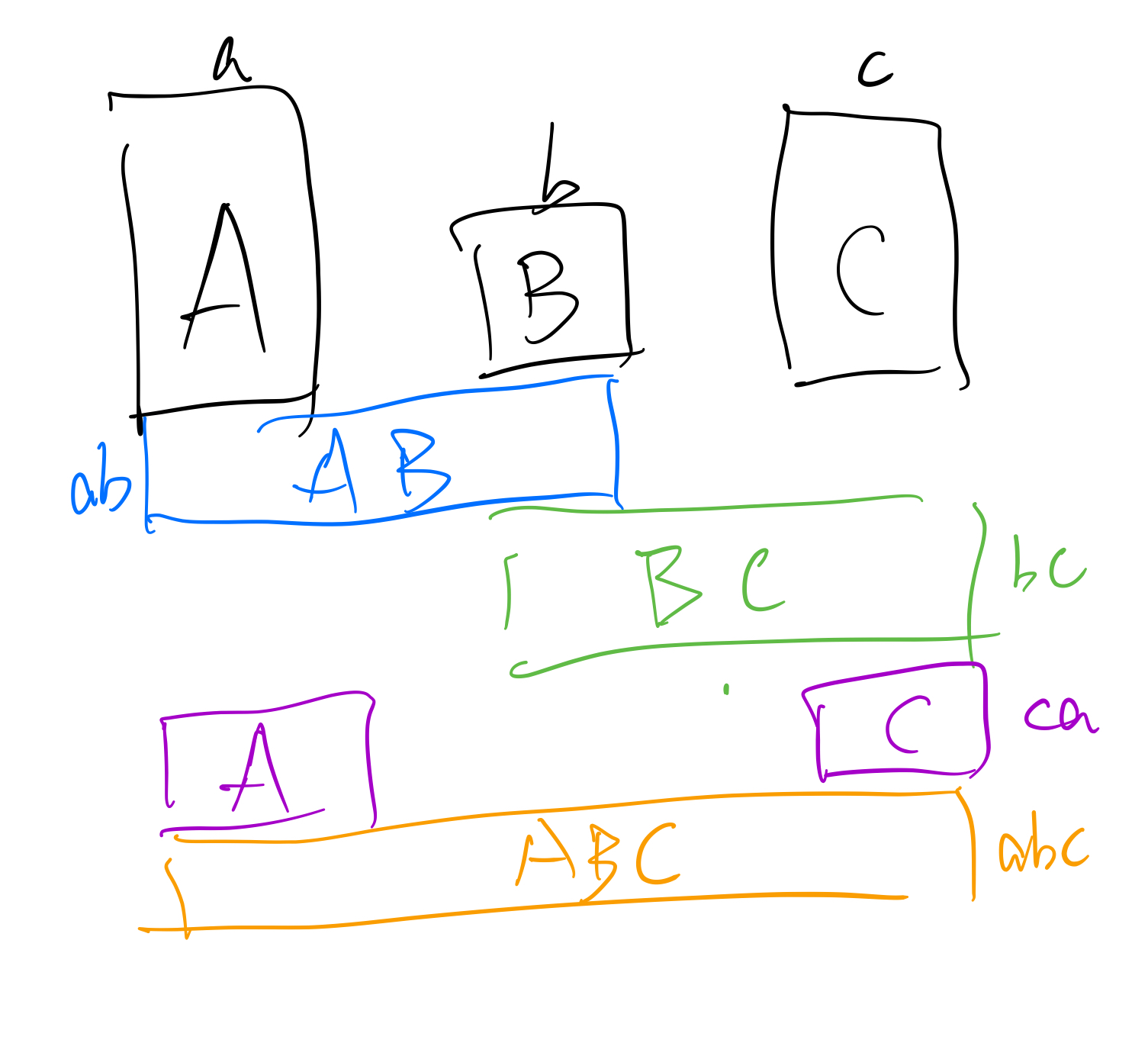
然后把A的因子个数 分为{A独有的因子的个数，仅AB共有的因子的个数，仅CA共有的因子的个数，ABC共有的因子的个数}

对B和C同样的处理，然后 就会发现，不过是个4*4*4的排列组合(因为不同的分化之间相互不重叠)，注意去重,就随便写都过了，毕竟O(4*4*4*100'000)

497D1B

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define rep(i,a,n) for (int i=a;i<n;i++)

int yzcnt[100010];

void init(){
  rep(i,1,100001)
    yzcnt[i]++;
  rep(i,2,100001){
    rep(j,1,100000/i+1){
      if(i*j<100001){
        yzcnt[i*j]++;
      }
    }
  }
}

int gcd(int a,int b){
  return b==0?a:gcd(b,a%b);
}

ll calc(ll *v1,ll *v2,ll *v3){
  if(v1 == v2 && v2 == v3){
    return (*v1)*(*v1+1)*(*v1+2)/6;
  }
  if(v1 == v2){
    return (*v3)*((*v1+1)*(*v1)/2);
  }
  if(v2 == v3){
    return (*v1)*((*v2+1)*(*v2)/2);
  }
  if(v3 == v1){
    return (*v2)*((*v3+1)*(*v3)/2);
  }
  return (*v1)*(*v2)*(*v3);
}

int ec(int a,int b,int c){
  return c+7*(b+7*a);
}

int main(){
  init();
  int t;
  cin>>t;
  while(t-->0){
    int v[3];
    scanf("%d %d %d",v,v+1,v+2);
    int gab= gcd(v[0],v[1]);
    int gbc= gcd(v[1],v[2]);
    int gca= gcd(v[2],v[0]);
    int gabc= gcd(gab,v[2]);

    // 计算每一个的仅有的部分
    /*0*/ll a = yzcnt[v[0]] - yzcnt[gab] - yzcnt[gca] + yzcnt[gabc];
    /*1*/ll b = yzcnt[v[1]] - yzcnt[gbc] - yzcnt[gab] + yzcnt[gabc];
    /*2*/ll c = yzcnt[v[2]] - yzcnt[gca] - yzcnt[gbc] + yzcnt[gabc];
    /*3*/ll ab = yzcnt[gab] - yzcnt[gabc];
    /*4*/ll bc = yzcnt[gbc] - yzcnt[gabc];
    /*5*/ll ca = yzcnt[gca] - yzcnt[gabc];
    /*6*/ll abc = yzcnt[gabc];

    // 用于4*4*4的枚举
    ll *slotA[] = {&a,&ab,&ca,&abc};
    ll *slotB[] = {&b,&bc,&ab,&abc};
    ll *slotC[] = {&c,&ca,&bc,&abc};

    // 用于上面枚举的去重
    int slotMaskA[] = {0,3,5,6};
    int slotMaskB[] = {1,4,3,6};
    int slotMaskC[] = {2,5,4,6};
    bool masks[7*7*7];
    rep(i,0,7*7*7){
      masks[i] = false;
    }

    // 枚举
    ll ans = 0;
    rep(i,0,4){
      rep(j,0,4){
        rep(k,0,4){
          int maskarr[] = {slotMaskA[i],slotMaskB[j],slotMaskC[k]};
          sort(maskarr,maskarr+3);
          int code = ec(maskarr[0],maskarr[1],maskarr[2]);
          if(!masks[code]){// 去重
            masks[code] = true;
            ans +=calc(slotA[i],slotB[j],slotC[k]);
          }
        }
      }
    }
    printf("%lld\n",ans);
  }

  return 0;
}

代码

497D1B

参考

493D1C 官方题解

493D1C Petr的代码

497D1B wavator超级宽的代码