Pinely Round 3

發表於 更新於 分類於 ， Disqus： 文章字數： 1.1k 所需閱讀時間 ≈ 4 分鐘
F2(组合数学)G()H()I()

https://codeforces.com/contest/1909

F2 - Small Permutation Problem (Hard Version)

问有多少个 1~n的排列$p$满足, 对于所有$a_i \ne -1$时:

  • $\mathrm{count}(p_{1\cdots i}\le i) = a_i$

范围

$n\in [1,2\cdot 10^5]$

$a_i \in [-1,n]$

个数$\bmod 998’244’353$

2s

256mb

我的思路

对于F1来说$a_i$是没有$-1$的, 那么$a_i$的变化只有$+0,+1,+2$三种

通过dp[i]=前i个限制满足,且只关心前面位置对于放置[1..i]的放置方案即可AC

而这里感觉要处理的就是,两个相邻非$-1$之间的$a_i \to a_j$的转移

有点想用生成函数,$[x^a]f_{i} =$前i个满足时,且第i个的对应个数为$a$的方案数

在转移的优化上,因为一旦$a \ne -1$,那么生成函数其它的系数全为$0$

所以 可以考虑幂次平移 $g_{i} = \frac{f_{i}}{x^a}$

而对于$a = -1$的找比它小的最后一个非$-1$的a来转换

但转移方程似乎会上到二阶导数,没推出简洁的式子

题解

可视化辅助:

$n \cdot n$的格子,横纵坐标$(i,p_i)$

有一些反向的”L”形状, 每个”L”形状里有固定数量的点, (F1中 宽度为1,至多两个点), 随着i增加遍历形状

把每个形状切割成 2个长方形,再遍历第一个长方形中的tokens

WLOG(不失一般性), 也是考虑相邻非-1之间的转换,

从$a_i\to a_j$,前置的转换的具体情况,在把L可填部分连接上以后是不影响L的形状的

因此可以知道”L”形状的所有长宽

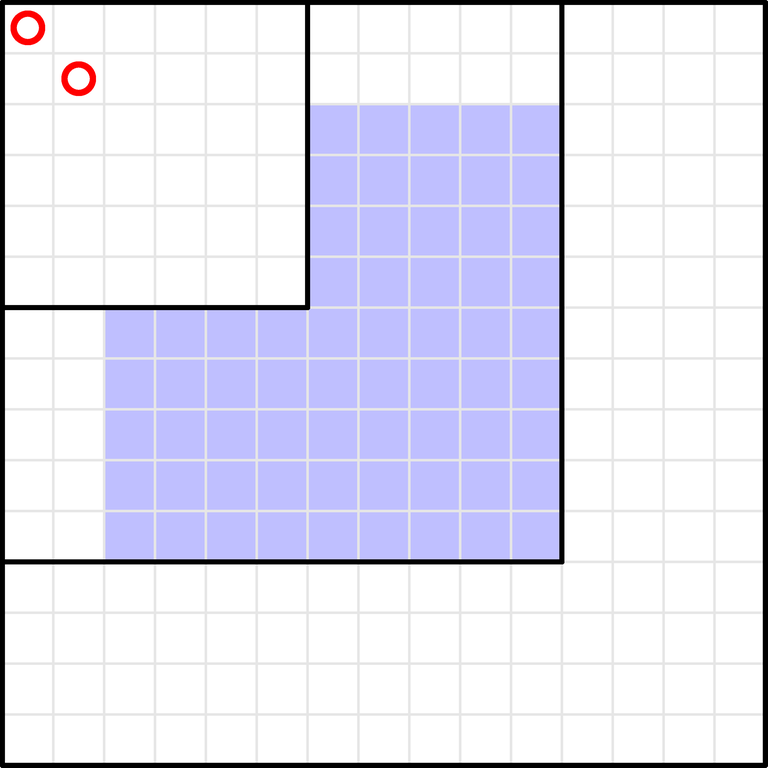
接下来是放$a_j-a_i$个点, 注意到的是点有2种,$\le i$和$>i$

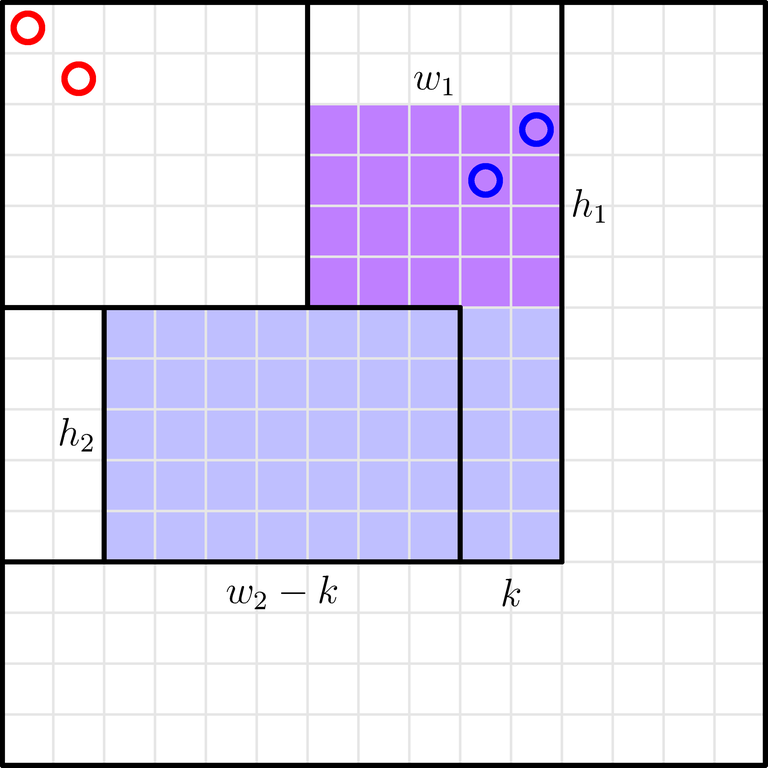
所以枚举$k\in [0,a_j-a_i]$个 $\le i$的点在上面的$w_1\cdot h_1$矩形中,

剩余$a_j-a_i-k$个点 在$(w_2 -k)\cdot h_2$矩形中

这就是简单的计数了

注意到所有的k的和$\le n$, 预处理binom,就没了

如果放弃掉图形,直接看逻辑意义其实也不难

也就是 前i个满足a_i,到前j个满足a_j的方案数

那么其实如同F1一样的想法dp的状态只关心 $\le i$的位置 和 $\le i$的值

对于空位置来说[i-a_i][j-i] 两段空位置

值一共放是$a_j-a_i$个, 枚举放k个$\le i$的到[j-i]的这段位置中

代码

https://codeforces.com/contest/1909/submission/238766567

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
#include <bits/stdc++.h>
typedef long long ll;
#define MOD 998244353
#define rep(i,a,n) for(ll i=(a);i<(ll)(n);i++)
#define per(i,a,n) for(ll i=(n);i-->(ll)(a);)
ll read(){ll r;scanf("%lld",&r);return r;}
const int N = 200000;
ll a[N+10]; // a[0] = 0
ll fac[N+10]={1};
ll ifac[N+10];
ll binom(int n,int m){return (m>n or m<0)?0:(fac[n]*ifac[m]%MOD*ifac[n-m]%MOD); }
ll mypow(ll b,int pwr){ll r=1;while(pwr){if(pwr&1)(r*=b)%=MOD;(b*=b)%=MOD;pwr/=2;};return r;}
int w(){
  int n = read();
  rep(i,1,n+1) a[i] = read();
  if(a[n] != n and a[n] != -1) return 0;
  a[n] = n;
  ll ans = 1; // dp[i] 只关心 <=i的位置和<=i的值
  int j = 0; // 上一个非0位置
  // 一共a个值,b个位置,选c个放置,有顺序
  auto _=[&](ll a,ll b,ll c){ return (c > a or c > b)?0:(binom(a,c) * binom(b,c) %MOD * fac[c]%MOD); };
  rep(i,1,n+1) if(a[i] != -1) { // j -> i, a[j] -> a[i], 空位置 [j - a[j]][i - j]
    if(a[i] < a[j]) return 0; // sum (a[i]-a[j]) <= n
    ll mul = 0;
    // k个值<= j的放在 [i-j]区间, 值(j, i]放在[i-a[j]-k]
    rep(k,0,a[i]-a[j]+1) (mul += _(j-a[j],i-j,k)*_(i-j,i-a[j]-k,a[i]-a[j]-k)%MOD )%=MOD;
    (ans *= mul) %= MOD;
    j = i;
  }
  return ans;
}

int main(){
  rep(i,1,N+1) fac[i]=fac[i-1]*i%MOD;
  ifac[N] = mypow(fac[N],MOD-2);
  per(i,0,N) ifac[i] = ifac[i+1]*(i+1)%MOD;
  int t = read();
  while(t--) printf("%d\n",w());
  return 0;
}

总结

F2

感觉 在转换想到相邻转换是没问题,但F2似乎没有预期的那么难,还不需要生成函数,就是图像化+计数,甚至统计的感觉好的化,不用图像化, 简单的数数就够了

比赛时没做出E,F2真的不应该,都是掌握的知识,而且F1的思路和F2完全一样,但是现场没反应过来,为我自己感到羞愧

参考

官方editorial: https://codeforces.com/blog/entry/123584