Atcoder arc139

發表於 更新於 分類於 ， Disqus： 文章字數： 2.1k 所需閱讀時間 ≈ 7 分鐘
C(构造),D(频率频次, 贡献统计, 二项式分布)

C

https://atcoder.jp/contests/arc139/tasks/arc139_c

nxm格子选尽可能多的点

让每个点(x,y)的(x+3y)互不相等

且每个点(x,y)的(3x+y)互不相等

n,m <= 1e5

题解

我的思路是, 这相当于做的线性变换

每个点变成 (x,y) => (3x+y,x+3y)

要结果的点 的横纵坐标互不相等

那么原来是矩形的点, 映射后变成了斜着平行四边形的点

然后想办法尽可能多的找点, 但是我可能点画得不算多, 没有找到规律

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
import matplotlib.pyplot as plt

x = []
y = []

for i in range(1, 10):
    for j in range(1, 10):
        x.append(3*i+j)
        y.append(i+3*j)

plt.plot(x, y, 'ro')
ax = plt.gca()
ax.set_xlim(0)
ax.set_ylim(0)
ax.xaxis.set_minor_locator(plt.MultipleLocator(1))
ax.yaxis.set_minor_locator(plt.MultipleLocator(1))
plt.grid(which='minor')
plt.show()

1

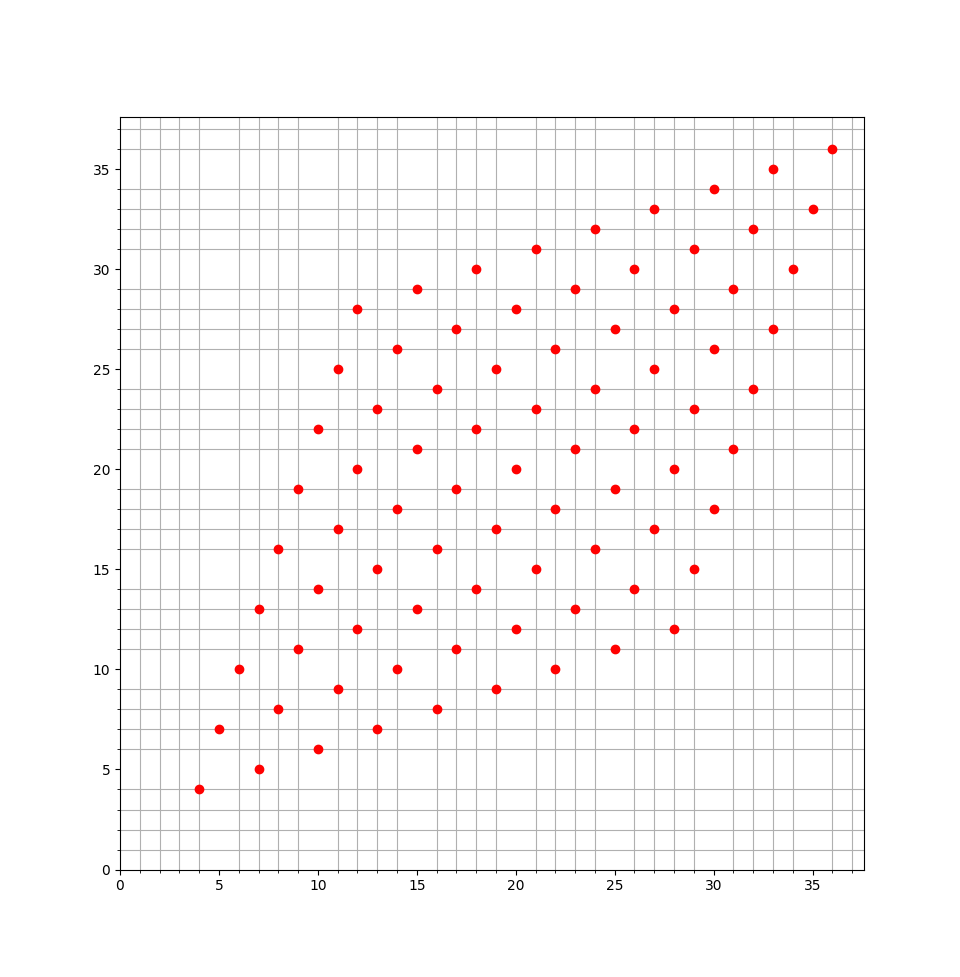
先考虑特殊情况足够大

那么对于 3x+y 有没有可能尽量排满

两种办法让3x+y 的增量为1

(x,y) => (x,y+1)

(x,y) => (x+1,y-2)

比较神奇的是

如果你考虑x+3y每次增加1的方案,是对称的

(x,y) => (x+1,y)

(x,y) => (x-2,y+1)

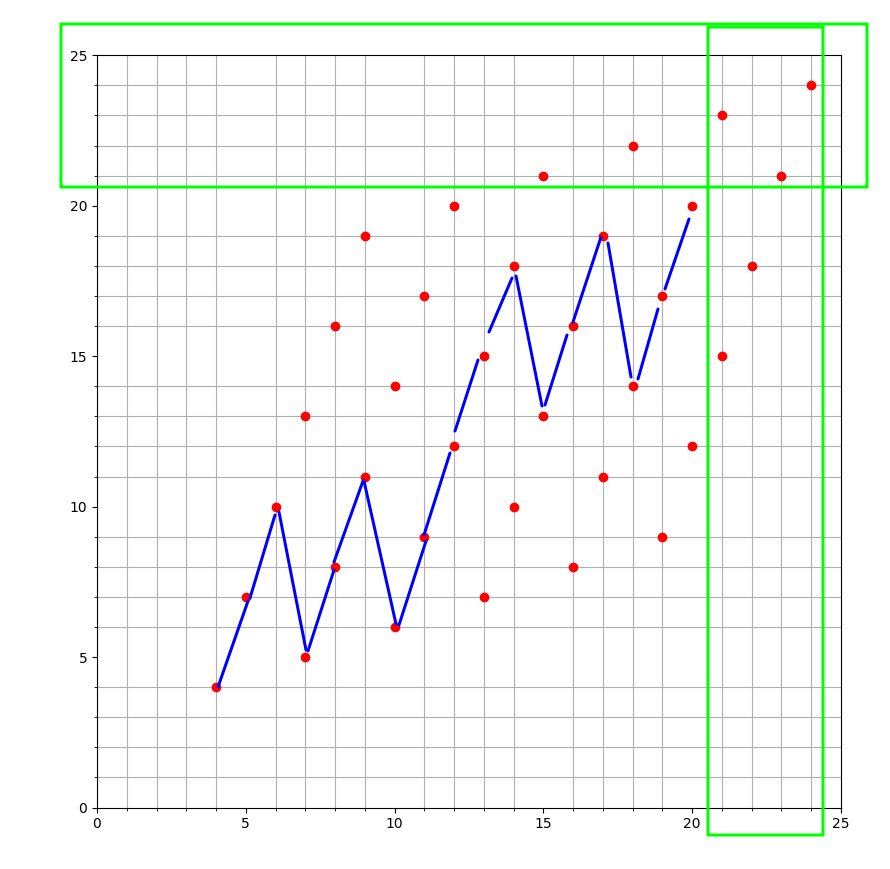
那么如图, 两个方法选的点(蓝色路线 和 绿色路线) 是一样的

2

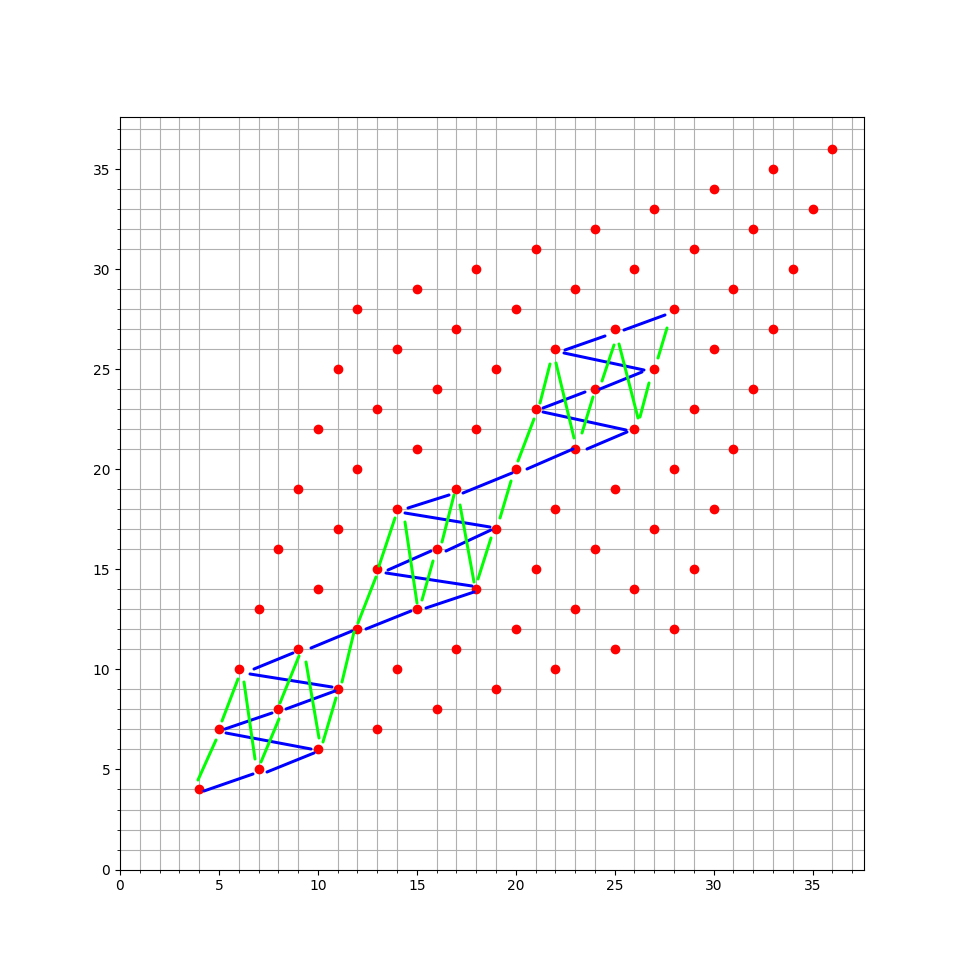
因此, 如果刚好 N=M, 且N是奇数, 就按照这个方法去选即可, 这样相当于把所有可能的(x+3y),(3x+y)的值都取到了

非一般情况, 首先N,M 是可以轮换

所以不妨设 N<=M

注意最大的个数,会被min(3n+m,n+3m) 限制, 也就是点的上界

但是如果短的边也是奇数的话

可以这样操作

3

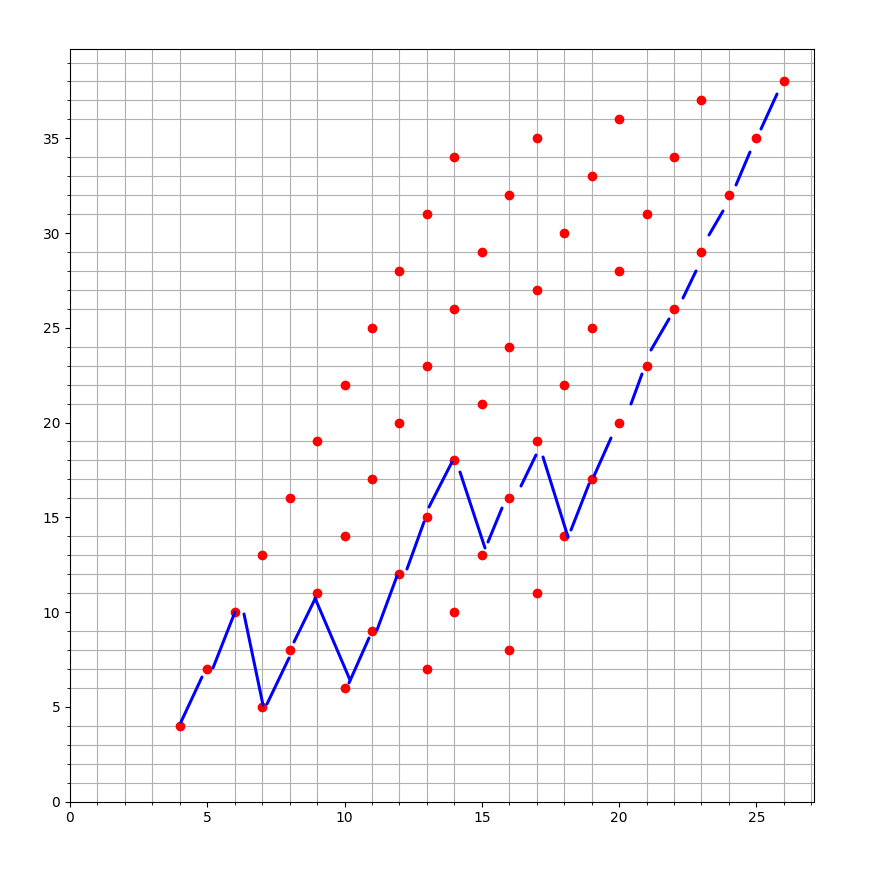
这样即满足题意, 又达到了上界

两边不等,但是短边是 偶数长度

5

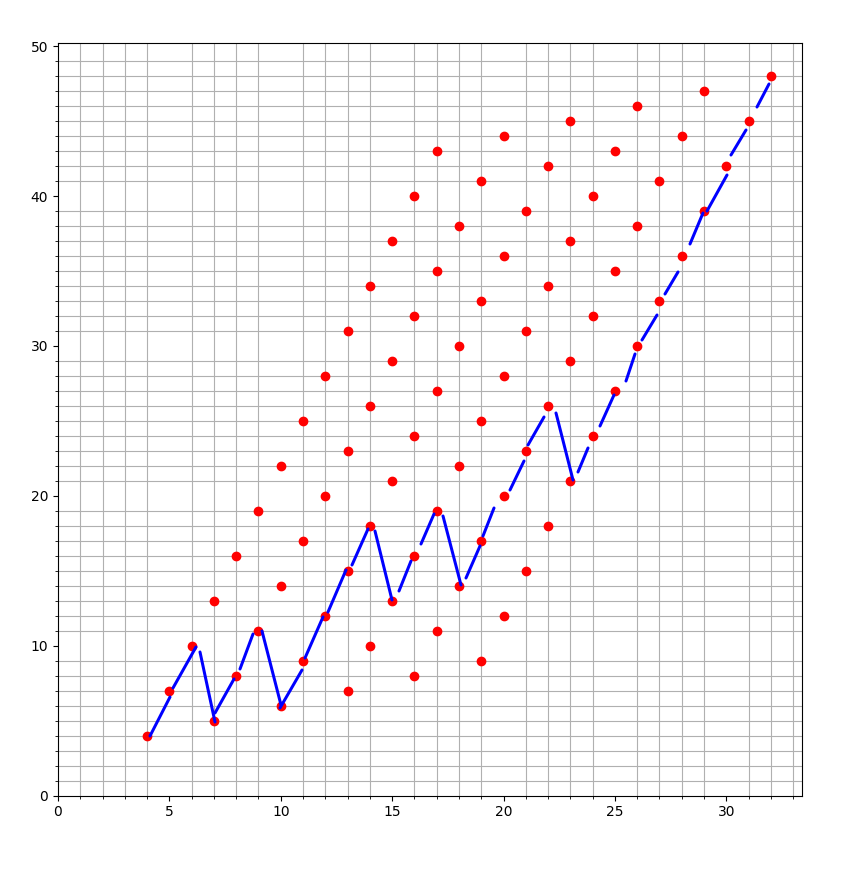
这样即满足题意, 又达到了上界

还有一个情况

两边相等,但是 是偶数长度

4

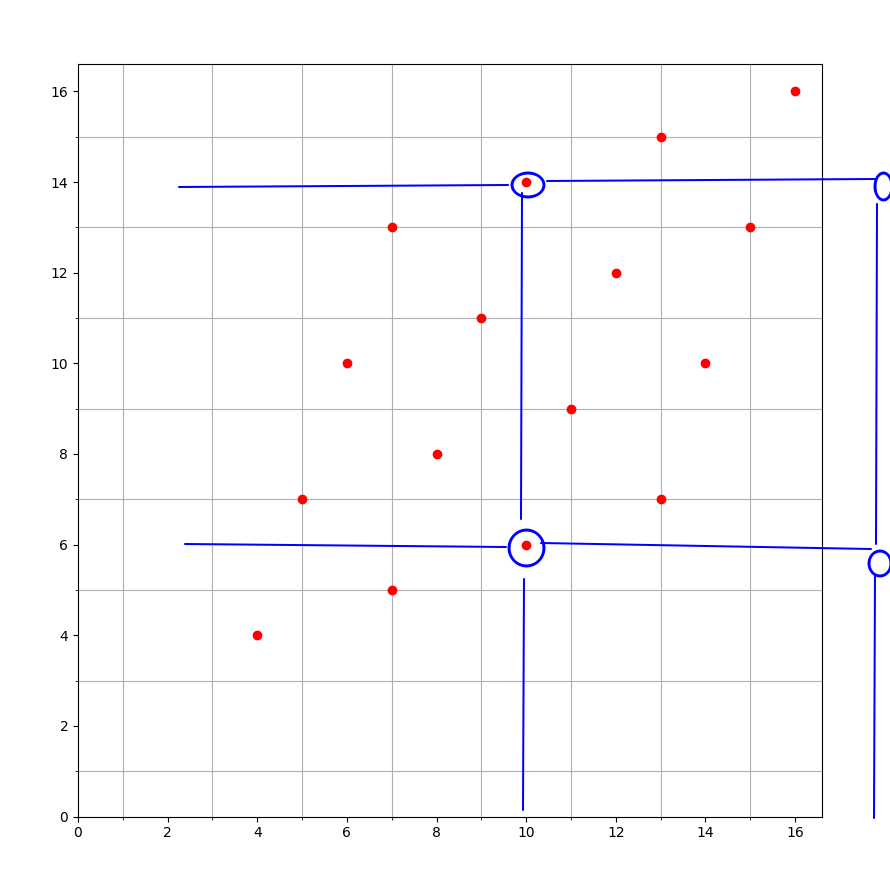
如图, 距离上界还差4个, 但是看起来按现有的选法最多再选3个

下面证明 就是差一个

首先如果 N=2 , 那么M=2 最多选取 NM = 3N+M-4个

对于 N >= 4,且为偶数

S = 从(3,1)开始, 通过多次 (+1,-3) / (+3,-1) 到达的所有点

注意到 这个集合中 其实就是 转换坐标轴后以 (3,1) 开始,同纵坐标,和同横坐标,反复关联的点

6

而这些点,在x上的可选值 为 N/2-1, y上的可选值为N/2, 也就是S中的点本身是互相影响的点,而这些点占了N/2个位置,最多却只能选N/2-1, 因此 总的上界也是比范围小一

所以 不论N=2还是N>=4 的偶数情况, 上述少选一个的方案 既能达到 又是上界

代码

(无)

参考

官方题解 https://atcoder.jp/contests/arc139/editorial/3863

Youtube官方 https://www.youtube.com/watch?v=tIdPBN2x6KU

D

https://atcoder.jp/contests/arc139/tasks/arc139_d

长度为n的有序数组a

每次操作, 选择[1~m]中的一个插入并保持有序, 删除下标为X的数(1-index)

进行k次操作的所有结果的剩余数组元素的和, 模 998244353

范围

n,m,k <= 2000

$X \in [1,n]$

$a_i \in [1,m]$

2s

1024MB

我的思路

如果知道 最后结果数组中, 位置i 为v 的出现次数,那么 最后只需要求和即可

cnt(a[i] == v)

注意到 a一直是有序的,也就是 cnt(a[i] == v) 也意味着 a[i..n] >= v

cnt(a[i] == v) = cnt(a[i..n] >= v) - cnt(a[i..n] >= v-1)

把指定位置等于 转化成 指定范围大于等于, 就能更容易进行状态转移了

dp[0..k][1..n][1..m]

dp[itr][idx][v] = 第itr次操作后, 从idx到n 都大于等于v的方案数

注意到 转移的系数和 itr 无关,所以可能可以矩阵快速幂

但是我没推出来

官方题解翻译

如果 对于$\forall v \in [1..m]$ 我们能找到结果中 $\leq v$ 的数出现的次数 的期望(频次 = 总次数 * 频率), 那么就能计算答案了(和上面我思路同理 都是 等于转化成 大于等于/小于等于)

题意转换:

对于一个指定的$v$

给定 $x \in [0,N]$

$x$的意义是初始数组中 $\leq v$的个数

操作: 概率$p = \frac{v}{m}$ 让x=x+1, 如果 $x\ge X$ , 让x=x-1

意义是 有概率$p$ 选择不超过$v$的数, 那么个数加一

如果 总个数 大于 删除下标, 那么 必定被删除一个, 那么个数减一

找到执行了$K$次操作后, $x$的期望值

也就是 剩下 $\leq v$ 的个数

注意到$|x - (X-1)|$ 会单调递减

换句话说, 如果 $初始x > (X-1)$ 那么$初始x \ge 最终x \ge (X-1)$

如果 $初始x < (X-1)$ 那么$初始x \leq 最终x \leq (X-1)$

$初始x$ 是从输入的a中统计的

如果我们指定了最终的x, 那么得到这个x的 概率可以用二项式系数和幂次得到

设 初始值为$x_0$, 最终为$x_1$

若 $x_0 \leq x_1 < X-1$

也就是$k$次 操作中 $x_1 - x_0$ 次增加了1, 其它时候全未增加

概率为 $C(k, x_1-x_0) \cdot p^{x_1-x_0}(1-p)^{k-(x_1-x_0)}$

若 $x_0 < x_1 = X-1$ (如果 都是$X-1$那概率就是1)

也就是$k$次 操作中 至少$x_1 - x_0$ 次增加了1, 其它时候任意

概率为 $\sum_{i=0}^{k-(x_1-x_0)} C(k, x_1-x_0 + i) \cdot p^{x_1-x_0 + i}(1-p)^{k-(x_1-x_0 + i)}$

看起来难算, 但是因为 上面的$x_1 \neq X-1$的和$x_1 = X-1$构成了所有情况, 所以实际上直接 1减去上面概率和就是剩下概率

对于$初始x_0$大于$X-1$的同理

其中组合数可以预处理,幂次可以快速幂

综上 可算

代码

https://atcoder.jp/contests/arc139/submissions/31271889

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
#include <bits/stdc++.h>
using namespace std;

typedef long long ll;
#define MOD 998244353
#define rep(i,a,n) for (ll i=a;i<(ll)n;i++)

ll a[2010];
ll pro[2010][2010]; // [v][cnt] 结果 <= v 的有cnt个的概率
ll c[2010][2010];

ll mypow(ll v,ll pwr){
  v=(v+MOD)%MOD;
  ll r = 1;
  while(pwr){
    if(pwr%2)(r*=v)%=MOD;
    (v*=v)%=MOD;
    pwr/=2;
  }
  return r;
}

// C(m,n) = m!/(n!(m-n)!)
ll C(ll m,ll n){
  if(n > m)return 0;
  return c[m][n];
}

int main(){
  rep(i,1,2005){
    c[i][0] = c[i][i] = 1;
    rep(j,1,i){
      c[i][j] = (c[i-1][j-1] + c[i-1][j])%MOD;
    }
  }

  ll n,m,k,x;
  cin>>n>>m>>k>>x;
  ll invm = mypow(m,MOD-2);
  x--; // 先减1
  rep(i,0,n){
    scanf("%lld",a+i);
  }
  sort(a,a+n);
  rep(v,1,m+1){
    int stx = 0;
    rep(i,0,n){
      if(a[i] <= v)stx++;
      else break;
    }
    if(stx == x){ // 结果必定 x
      pro[v][x] = 1;
      continue;
    }
    // p = v/m
    ll p = v * invm %MOD;
    rep(endx,0,n+1){
      if(stx < x){ // stx <= endx <= x
        if(stx <= endx && endx < x){
          // C(k,endx-stx) * p^(endx-stx) * (1-p)^(k-(endx-stx))
          pro[v][endx] = C(k,endx-stx) * mypow(p,endx-stx) %MOD * mypow(1-p,k-(endx-stx)) % MOD;
        }
      }else { // stx > x => stx >= endx >= x
        if(stx >= endx && endx > x){
          // C(k,stx-endx) * (1-p)^(stx-endx) * p^(k-(stx-endx))
          pro[v][endx] = C(k,stx-endx) * mypow(1-p,stx-endx) %MOD * mypow(p,k-(stx-endx)) % MOD;
        }
      }
    }
    // 最后处理 (endx == x) , 等于 1-其它概率和
    pro[v][x] = 1;
    rep(endx,0,n+1){
      if(endx == x)continue;
      (pro[v][x] -= pro[v][endx])%=MOD;
    }
  }
  ll leqv[2010] = {0};
  ll ans = 0;
  rep(v,1,m+1){
    rep(cnt,0,n+1){
      (leqv[v] += cnt*pro[v][cnt]%MOD)%=MOD; // 期望长度 = sum{期望*长度}
    }
    (ans += v*(leqv[v] - leqv[v-1]) %MOD)%=MOD; // count( == v) = count(<= v) - count(<= v-1)
  }
  printf("%lld\n", ((ans * mypow(m,k)%MOD)+MOD)%MOD); // 频次 = 总次数 * 频率
  return 0;
}

总结

相对于以前不会 count(x = v) = count(x >= v) - count(x >= v+1) = count(x <= v) - count(x <= v-1) , 已经算是有进步,能想到转换了

  1. 但是 对于上面 转换成概率 和 小于统计的想法还是不够, 一个是 想用坐标表示而不是明确的值的分界线表示, 题解就没有坐标作为键,只是把坐标作为值

  2. 虽然从频次上也能算,但是上到概率,推概率公式,算出概率再转换成频次都会容易进入思路, 需要增加 频次和概率之间的转换意识

参考

官方题解 https://atcoder.jp/contests/arc139/editorial/3860

Youtube官方 https://www.youtube.com/watch?v=tIdPBN2x6KU