Atcoder abc275

發表於 2022-10-29 更新於 2024-10-23 分類於 Atcoder ， ABC Disqus：文章字數： 3.5k 所需閱讀時間 ≈ 12 分鐘

G(数学,计算几何)Ex(二叉树,单调队列,DP,树上DP,凸函数,树上启发式合并)

https://atcoder.jp/contests/abc275/tasks

G - Infinite Knapsack

n种物品, 每种无限多个

第i种, 重ai,体积bi,价值ci

f(X) = 总重量<=X,总体积<=X的最大价值

可证明 lim_{x->infty}f(X)/X 的极限存在, 求极限

范围

n 2e5

ai,bi,ci [1e8,1e9]

1024mb

我的思路

感觉就一个很数学的题

考虑3元组, (a,b,c) 若 a >= b, 等价于a个(a/a,b/a,c/a)

若 a < b, 等价于a个(a/b,b/b,c/b)

于是分成两种

$(1,p\le1,c_0),p=b_0/a_0$

$(q\le1,1,c_1),q=a_0/b_0$

而实际上未来增长只会是这两种按一个比例的和

$(t_0,pt_0,c_0t_0) + (qt_1,t_1,c_1t_1)$

$t_0 + qt_1 = pt_0+t_1 $

$t_0 = t_1 (1-q)/(1-p)$

$c_{0,1} = (c_0t_0 + c_1t_1)/(t_0 + qt_1)$

$= (c_0(1-q)/(1-p) + c_1)/((1-q)/(1-p)+ q)$

$= (c_0/(1-p)+c_1/(1-q))/(1/(1-p)+q/(1-q))$

$ans=\max(c_0,c_1,(c_0(1-q)+ (1-p)c_1)/((1-q)+ (1-p)q))$

问题是两两计算的话为n^2

稍微改一下

$1,p < 1,c_0$

$1,q > 1,c_1$

$pt_0+qt_0=t_0+t_1$其中$t_0,t_1 > 0$ 即$t_0 = t_1 \frac{q-1}{1-p}$

$c_{0,1}=\frac{c_0t_0+c_1t_1}{t_0+t_1}$

$= \frac{c_0\frac{q-1}{1-p}+c_1}{\frac{q-1}{1-p}+1}$

$= \frac{\frac{c_0}{1-p}-\frac{c_1}{1-q}}{\frac{1}{1-p}-\frac{1}{1-q}}$

也就是 $(\frac{1}{1-\frac{b_i}{a_i}},\frac{\frac{c_i}{a_i}}{1-\frac{b_i}{a_i}})$ 这些点之间的最大斜率

n个点之间找最大斜率

但注意到的是是由第4向限和第1向限的点, 并不是两两之间, (因为两两之间的话相当于$t <0)

直接考虑分别两坨点的凸包

双指针???? 不会了

题解

类似的, 变成达到价值为1, 需要的 max(weight,volume) 的最小值,每个可取非负实数个

所以考虑(A/C,B/C,C/C)

平面上画(A’,B’)

那么其实两点之间的线段就是两点可以变成的点(加权平均数)

一个点对应的答案是max(x,y)

而一条线段MN 和 y=x 的交点O, 有性质MN上的点P, 在MO一侧和在NO一侧, 总有一个坐标大于$O_x,O_y$

所以就是求所有点与$x,y$的交

对所有点求凸包, 显然任意两点的线段在凸包中(凸包的性质)

因此求凸包上与y=x的交点,即可

代码

https://atcoder.jp/contests/abc275/submissions/36129413

#include <bits/stdc++.h>
typedef long long ll;
#define rep(i,a,n) for (ll i=a;i<(ll)n;i++)
ll read(){ll r;scanf("%lld",&r);return r;}
template<class T>
using Point = std::pair<T, T>;

template<class T>
class ConvexHull{
public:
  std::vector<Point<T>> lower;
  std::vector<Point<T>> upper;
  Point<T> sub(const Point<T>&a,const Point<T>&b)const{ // return a-b
    return {a.first-b.first,a.second-b.second};
  }
  T cross(const Point<T>& a,const Point<T>& b,const Point<T>& c)const{ // (a-b) x (c-b)
    auto [x0,y0] = sub(a,b);
    auto [x1,y1] = sub(c,b);
    return x1*y0 -x0*y1;
  }
  ConvexHull(std::vector<Point<T>>&p) {
    sort(p.begin(),p.end());
    {
      std::vector<Point<T>> v=p; // 逆时针弧
      for(Point<T>p : v){
        while(lower.size() >= 2 && cross(lower.rbegin()[1], lower.back(), p) <= 0) lower.pop_back();
        lower.push_back(p);
      }
    }
    {
      std::vector<Point<T>> v=p; // 顺时针弧
      for(Point<T>p : v){
        while(upper.size() >= 2 && cross(upper.rbegin()[1], upper.back(), p) >= 0) upper.pop_back();
        upper.push_back(p);
      }
    }
  }
  T cxy(const std::vector<Point<T>>&v) const{
    T ret=20;
    rep(i,1,v.size()){
      auto [x0,y0]=v[i-1];
      auto [x1,y1]=v[i];
      auto dx=x1-x0;
      auto dy=y1-y0;
      if(std::abs(dx-dy)<0.001)continue; // 分母为0 平行y=x
      auto xy = (y0*dx-x0*dy)/(dx-dy);
      if((x0-xy)*(x1-xy) < 0) ret=std::min(ret,xy); // 在两点之间
    }
    return 1/ret;
  }
  T cut()const {
    return std::max(cxy(lower),cxy(upper));
  }
};

int main(){
  int n=read();
  std::vector<Point<double>>points;
  double ans=0;
  rep(i,0,n){
    ll a=read(); // [1e8,1e9]
    ll b=read();
    ll c=read();
    ans=std::max(ans,c*1.0/std::max(a,b));
    points.push_back(std::pair{a*1.0/c,b*1.0/c}); // [0.1,10]
  }
  ConvexHull<double> ch(points);
  if(n==1){
    printf("%.15lf\n",ans);
    return 0;
  }
  ans=std::max(ans,ch.cut());
  printf("%.15lf\n",ans);
  return 0;
}

Ex - Monster

给定长N数组A

每次选区间 [l..r], 花费代价max(B[l..r]), 让A[l..r]-=1

让所有$A[i] <= 0$ 的最小代价和

范围

N 1e5

ai,bi [1,1e9]

1024mb

我的思路

显然每次全区间减一是一个方案, 所以上限是 max(Bi) * max(Ai)

那么一个操作方案, 交换顺序也会有同样的最终的A和代价, 所以顺序不影响结果和代价

不会有相邻的操作

[a...b][b+1..c]

这样的代价是max(B[a..b])+max(B[b+1..c]), 而直接B[a..c] 代价=max(B[a..c])=max(max(B[a..b]),max(B[b+1..c]))

A[i] >= A[i+1], B[i] >= B[i+1], 那么必定每次选i的时候能白带上i+1, 因为至少A[i]次操作在A[i]上,且选的值>=B[i]>=B[i+1], 所以如果没有选i+1,那么带上i+1 不会更差

因此这种i+1 直接干掉, A[i]>=A[i-1]且B[i]>=B[i-1]同理

因此数组变成若 A[i] > A[i+1] 则B[i] < B[i+1]

简而言之, 若A比相邻的大于, 则B比相邻的小于

也就是 A的下降对应B的上升, A的上升对应B的下降

感觉对区间的A最大尽心贪心? 选它大于相邻最小次B?

但似乎也不对, 下面这样的话,可能一次把所有大的-1 比单独的每个处理更优

A: 大小大小大小大小大小大小大小
B: 小大小大小大小大小大小大小大

A: 2 1 2 1 2 1 2 1 2 1 2 1 
B: 1 2 1 2 1 2 1 2 1 2 1 2

多次 n * 1
一次 2

考虑

1	[l...m][m+1..r]

切分

那么对于m来说至少在m上操作了A[m]次

m+1来说至少在m+1上操作了A[m+1]次

那么这些次之间顺序不重要, 假设分别排序为vec0,vec1

那么每次合并两个, 就是左右中大的那个, 考虑从大到小匹配, 每次有小的代价的盈余

= 左+右-盈余

问题是, 这样左右状态那是 [总代价, vec], 1e5 的1e5次方?

再来

1	dp[i] = [总代价, vec]

上面有不会有相邻区间的选择

那么考虑dp[i+1] , 从状态转移, 就是

新的vec最大的a[i+1]个需要大于等于B[i]

所以一共要最大A[i]个, 然后

对于所有i, 前A[i]个大于等于B[i]

就没了?

其实并不对, 这里应该是至少a[i+1]个, 然后每个需要>=Bi, 也就是当个数不变的话, 超过a[i+1]的也会被影响

1 2	Al -> Ar 单调递减 Bl -> Br 单调递增

初始是vecl 结束是vecr

显然 A[r] <= len(vecr) <= len(vecl)

vecr[i] = max(vecl[i],B[r]) 因为中间都比B[r]小不影响结果

但是中间变化时可能有大于len(vecr)的改变 vec的值

感觉也不行

考虑

1 2	A: 1e9 1 1e9 1 1e9 1 1e9 1 B: 1 1e9 1 1e9 1 1e9 1 1e9

这样的话, 需要约 (NAi)次, 所以次数/和光是这个维度都过于大

问题在于一个局部的峰肯定是单独处理峰更好, 而非局部的多个峰同时处理可能优于单个处理

而两个峰决定一起处理, 相当于把两个中低的高度等高的全部合并成一个, 代价为最低的B[i]

x
 x
  x   x  <-----------A
   x x
    x

    x    <-----------B
   x x
  x   x
 x 
x

就是找不出局部性啊…

题解

如果选的[l..r]的代价为b, 而[l-1..r] 或者[l..r+1]的代价依然是b, 那么就考虑更长的, 显然左右扩展的距离互不影响

也就有对于任何选的区间[l..r],

B[l-1] > 所有[l..r]

B[r+1] > 所有[l..r]

为了方便边界,可以假设两头B无限大,而A为0

这样的话, 考虑区间最大值在i取到, 那么对应的左右[li,ri]就唯一了!!!!!, 根据Bi来决定

所以只可能有 n种可选区间

考虑构建二叉树, 以最大的Bi为根(那么它其实就是对应(1,n), 左子树就是左边最大的为根, 右子树就是右边最大的为根,而区间就从i划分开了

有性质树上节点比子节点大, 在当前节点和子树中只有当前节点覆盖了i

所以在树上设计DP

dp[i][j] = 第 Bi对应的区间 [li..ri], A[li..ri] -=j 的答案(只考虑[li..ri]

答案=dp[最大Bi的下标][0]

如果区间长度为1即li==ri, 有 $dp[i][j]= \begin{cases} (A_i-j)B_i & (0\leq j\leq A_i) \\ 0 & (A_i\leq j), \end{cases}$

否则考虑对当前节点使用$k(\ge \max(A_i-j,0))$次(至少覆盖当前, 而对左右来讲可能额外覆盖), 然后就是左右子树的递归问题

$dp[i][j]=\displaystyle\min_{\max(A_i-j,0)\leq k} \lbrace kB_i+ dp[\mathrm{child}_ l][j+k]+dp[\mathrm{child}_ r][j+k]\rbrace.$

而随着$k+=1$ 增量$B_i+(dp[x][j+k+1]-dp[x][j+k])+(dp[y][j+k+1]-dp[y][j+k])$ 在单调递增

归纳法: dp[i][] 随着j 单调递减, 且增量([j+1]-[j])单调递增(下凸函数)

存在一个$k$和$k+1$在正负交界的位置

再换句话说, dp[i][j] 不影响min中的函数的’形状’, 而只是影响k的范围和对函数的平移, 而取min就是对最小值的平移

设是$j_{\min}$让$dp[\mathrm{child}_ l][j]+dp[\mathrm{child}_ r][j]$取到下凸函数的最小值

那么就是看$j+k = j_{\min} \ge A_i$能不能取到, 于是

$dp[i][j]=\begin{cases} (j_{\min}-j)B_i+ dp[x][j_{\min}]+dp[y][j_{\min}], j\le j_{\min} \\ dp[i][j]=dp[x][j]+dp[y][j], j\ge j_{\min}\end{cases}$

多线段优化(Polyline optimization

上面这样搞还是需要每个树上的点是一个左边一次函数,右边多点的下凸, 还是O(NAi)的,而且还有左右凸函数合并的过程

考虑j的取值, 显然 j >= max(A[l..r]) 时, $dp[i][j]=0$, 然而$A_i$很大

考虑维护斜率(斜率变化点) 来维护,这样最多N个点, 还是$N^2$

而实际上每个点等于左右儿子的合并, 如果每次轻儿子向重儿子合并, 那么就只用操作$O(n log n)$个点

而如果能把上面公式转化成合并前后是不动点, 那么就可以实现了, 现在问题是有什么办法

让 dp[child l][...] 和 dp[child r][...] 的合并前后是不动点

先说函数加和, 如果记录的是相邻增量的差, 那么就可以简单的合并!

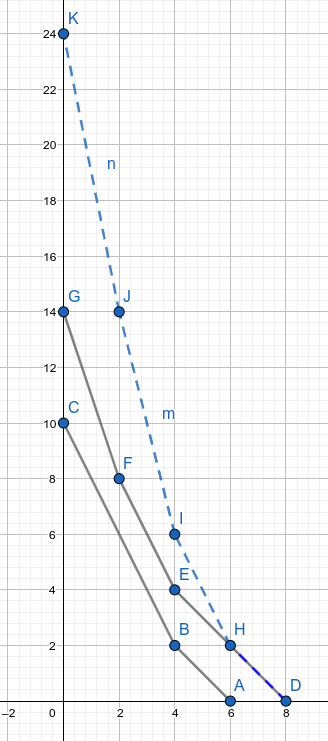
如图, 蓝色虚线是两个黑色的加和

其实从数学的角度讲, 两个按位置加和去做任意与加满足分配的运算比如导数都可以拆分

而直接记录点, 斜率的问题就是, 还需要改, 比如F变成J

而如果是记录前后斜率差, F变成J是不会变化的, 只有B+E=I这种共点需要加一下, 所以把小的向大的合并,只需要做小的次数

不妨记左右儿子合并后的为$f$

而对于 dp公式

$dp[i][j]=\begin{cases} (j_{\min}-j)B_i+ f[i][j_{\min}], j\le j_{\min} \\ dp[i][j]=f[i][j], j\ge j_{\min}\end{cases}$

也就是需要把左边一段变成斜率为$-B_i$, 这可以直接从左向右枚举

因为如果枚举到了要么停止要么删除,而停止最多一次,删除的点不超过加入的点

所以总的均摊的左侧枚举就是O(N)

因此从数据结构上

记录 ((点0的y值,斜率), map[点]=斜率差)

而实际上, 点0的具体值只有最后才需要, 所以可以全部记录斜率, 只是map[0] 表示的是直接的斜率而不是斜率差

代码

https://atcoder.jp/contests/abc275/submissions/36145016

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define rep(i,a,n) for (ll i=a;i<(ll)n;i++)

ll read(){ll r;scanf("%lld",&r);return r;}
const int MAXN = 1e5 + 10;

struct Data{
  map<int,ll> d; // diff[idx] = 斜率差
  ll k0; // 0处的斜率
  Data(): k0(0) {}
  void clear(){ d.clear(); k0 = 0;}
  void merge(Data &o){
    k0 += o.k0;
    if(d.size() < o.d.size()) d.swap(o.d); // C++ O(1), dsu on tree
    for(auto [p,x]: o.d) d[p]+=x;
    o.clear(); // MLE
  }
  void reg(ll b) { // find  b+ 斜率=(tot+斜率差前缀和) >= 0
    while(b+k0 < 0){
      auto it = d.begin();
      if(b+(k0+it->second) < 0){ // 增量为负
        k0 += it->second;
        d.erase(it);
      } else { // found 增量为
        it->second -= (-b)-k0;
        k0 = -b;
      }
    }
  }
  ll get(void) const {
    ll res = 0;
    for(auto t: d) res += t.first * t.second;
    return res;
  }
};

int a[MAXN], b[MAXN];
array<int,2> lr[MAXN]; // lr[i] = {left, right}, 左边右边比它大的下标
Data f[MAXN];

void dfs(int u) { // 树上DP
  f[u].k0 = -b[u];
  f[u].d[a[u]] = b[u]; // kBi, 一定要消耗的Ai
  for(int v: lr[u]) if(v) { // + left child diff[] + right child diff[]
    dfs(v);
    f[u].merge(f[v]);
  }
  f[u].reg(b[u]);
}

int main() {
  int n=read();
  rep(i,1,n+1)a[i]=read(); // 1-index, 0 表示没有儿子
  rep(i,1,n+1)b[i]=read();

  vector<int>stk={}; // 单调栈 下标
  rep(i,1,n+1){
    while(stk.size() && b[stk.back()] < b[i]){
      lr[i][0] = stk.back(); // left
      stk.pop_back();
    }
    if(stk.size()) lr[stk.back()][1] = i; // right
    stk.push_back(i);
  }
  dfs(stk[0]);

  printf("%lld\n",f[stk[0]].get());
  return 0;
}

总结

计算几何方向对了, 但是题意转化不尽人意, 搞出了需要找斜率的问题, 而题解里的转化成交点就显然很多了

考虑区间性质而不是相邻的性质, 这样一下就降低到只有n个区间,还是靠区间最大值划分的, 感觉似乎几次区间最大值都是类似的建立树,应该建立条件反射了

然后就是凸函数一类的斜率维护和函数合并,不动点的知识了

感觉这次的Ex虽然是个铜牌3210分的题, 但是对我来说都是之前补abc学过的知识点了没新知识点, 而我还是自己没搞出来, 甚至卡在第一步了, 哎

参考

官方题解