Atcoder abc272

發表於 更新於 分類於 ， Disqus： 文章字數： 5.1k 所需閱讀時間 ≈ 17 分鐘
G(数论)Ex(概率论,生成函数,多项式,多点求值,容斥原理,二项式反演,DP)

https://atcoder.jp/contests/abc272/tasks

G - Yet Another mod M

给长n数列A, distinct( ai != aj)

问是否存在 m \in [3,1e9]

使得 a[i]=a[i]%m 后,

有一半以上的数为某个x,(存在x使得x的个数 > 非x的个数)

范围

n 5000

ai 1e9

2s

1024mb

我的思路

感觉又是数论什么的, 不过这个n 5000 不知道是有什么n^2的说法吗

首先假设 能有x(m) 满足

显然 若p为m的因子

那么 这些 xi%m == x(m) 的 对应 xi%p = (xi%m)%p = x(m) %p 依然满足

所以只用考虑 质数 和 2 * 质数, 又因为2*质数 如果合法,则质数合法, 当为2^幂次时, 校验4即可

所以 只用考虑 质数

如果本来就有数字次数大于一半, 那么随便取

否则必定会让原来不等的两个数相等

考虑两个不等的数 ai,aj

ai % m == aj % m

(ai-aj) %m = 0

所以枚举质因子

但这样是 n^2 sqrt(ai) n

感觉并过不了? 上质因子拆解模版?

还是先收集完(ai-aj)

然后同时进行质因数查找

关键验证还需要n

(ai-aj)%m == 0 等价与 它们mod m后相等

换句话说, 收集ai-aj 后

如果 有t > n/2个值相等

那么两两成边 t(t-1)/2 条边, 即 ai-aj 需要 >= t(t-1)/2

这样的话 直接在收集后 的ai-aj 中枚举m????(O(max(ai/2)))

不会

题解

同样 |Ai-Aj| 是M的倍数

可以枚举 约数

反复 靠 概率 乱搞…..

Crying

一定有相邻的被选, 或者n=奇数, 间隔一个选一个

因此 M 一定是 某个|A_{i+1}-A{i}|的因数, 或者是 gcd(|A_{奇+2}-A_{奇}|

同上, 只用校验质数和4

注意到 sum d <= 1e9

而这里 复杂度是 (sum sqrt(d)) = sqrt(ai d) 能找出所有可能的质因数

O(质数个数 * 校验) = (9 * n) * n

O(sqrt(ai d) + 9 n^2)

注意到这里distinct 说明 不会有相等, 所以 相邻的差也不会为0

代码

https://atcoder.jp/contests/abc272/submissions/35948377

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
#include <bits/stdc++.h>
typedef long long ll;
#define rep(i,a,n) for (ll i=a;i<(ll)n;i++)
ll read(){ll r;scanf("%lld",&r);return r;}

int n,a[5010];
bool check(int u){
  int val=0;
  int cnt=0;
  rep(i,0,n){ // 经典匹配法
    int A=a[i]%u;
    if(cnt==0){
      val=A;
      cnt=1;
    }else{
      if(val==A)cnt++;
      else cnt--;
    }
  }
  if(cnt){
    cnt=0;
    rep(i,0,n)cnt+=(a[i]%u==val);
    if(cnt>(n/2)){
      printf("%d\n",u);
      return true;
    }
  }
  return false;
}
int main(){
  n=read();
  rep(i,0,n)a[i]=read();
  std::sort(a,a+n);
  if(n&1){ // 奇数个 隔一个选一个
    int g=0;
    rep(i,2,n)if(i%2==0)g=std::__gcd(g,a[i]-a[i-2]);
    if(g>=3){
      printf("%d\n",g);
      return 0;
    }
  }
  std::unordered_set<int>S;
  S.insert(4);
  rep(i,0,n-1){ // 相邻a[i+1] a[i]被选
    int d=a[i+1]-a[i];
    rep(j,2,d+1){ // O( all j ) = sqrt(d ai)
      if(j*j>d)break;
      if(d%j==0){
        if(j>2)S.insert(j);
        while(d%j==0)d/=j;
      }
    }
    if(d>2)S.insert(d);
  }
  for(auto u:S)if(check(u))return 0;
  printf("-1\n");
  return 0;
}

Ex - Flipping Coins 2

n 个硬币

初始都正面朝上

给定长n的序列A包含0..N-1

然后 会等概率选 A的一个排列, A[p[]]

第i次(0-index), 把 硬币[i … i + A[p[i]]] 翻转, 超界取mod

翻转n次后, 得到朝上的硬币个数的价值

问: 得到的价值的期望值 mod 998244353

范围

n 2e5

10s

1024mb

我的思路

一上来, 想的就是 map[处理前的状态][剩余可选ai] = 次数

但这显然大得离谱

稍微缩小一下状态就是 可以根据max(ai) 推得哪些 位置不再会变,然而这样对数量级影响来说没卵用

然后发现 如果min(ai) = t

那么意味着从每个开始都 翻转了长度 > t个

而注意到 虽然a[p[]] 会影响结果, 但是对于给定的a[p[]] 来说, 先a[p[i]] 还是先a[p[j]] 不会影响

所以如果t>=1等价于所有 a[i]-=2, (a[i]=-1表示不翻转)

这样可以让翻转的长度最小变为1(a[i]==0)或0(a[i]==-1)

对于最大最小差距大的情况 似乎并没什么卵用

上面注意到 实施翻转的顺序 并不会影响结果

换句话说, 每个位置其实是等价的,

那么一个位置被覆盖的奇偶性%2 的期望 * n 就是答案了

那么为了避免循环, 考虑说 最后一个位置被奇数个,偶数个覆盖的概率

而一个a[i] 让 最后一个n 被覆盖的概率就是 长度/n, 这个概率对应的是的奇偶交换

所以ans = n * ( prod (长/n) or 1-prod(长/n)), 根据n的奇偶性来决定

就没了?

有点问题, 首先可以看到 长可以-2, 让上面式子不等

问题出在, 长Ai放在pi 和长Aj放在pi 不能同时发生

所以 要计算的是 同时cover的翻转概率 显然不能 prod 分别的概率

其实是 有偶数个 a[i]-p[i] >= 0 的概率

题解

下面$A,B,C$全是 1-index

问题转化

首先A的顺序不影响, sort(A)

和我分析的一样 所有硬币朝上概率等价, 不妨直接算最后一个硬币朝上的概率 = 朝上的排列方案数/n!

F(K) = 让最后一个硬币翻转K次的排列方案数

F(K) = 恰好有K个(P[i] >= N-1-Ai) 的排列方案数

为了方便 $B_i=N-1-A_i$, 所以B是非严格递减

容斥原理

上面的F(K)难以直接计算

找满足 集合S中所有i满足 $P_i\ge B_i$ 的 排列的个数$Count(S)$

令$G(L) = \sum_{S\subset\lbrace 1,2,\cdots,N\rbrace |S|=L} Count(S)$

$G(L) = \sum_{L\le K}\binom{K}{L} F(K)$, 一个具体的恰好K次的方案P, 在F(K)中贡献1, 而这K个满足的不等式中任选L个构成的集合S也是满足, 而 这个 方案P 通过 S 在 G(L=|S|) 贡献1

据说在arc140f题解中(我还没补) 有二项式反演

所以如果能有G, 那么可以二项式反演算F

$F(K) = \sum_{K\le L}(-1)^{L-K} \binom{L}{K} G(L)$

复杂度$O(n \log n)$

二项式反演

演绎推理是我们在数学中经常遇到的一些方法。对于数列来说，通过原数列计算出新的数列叫作演绎，而通过计算出的数列反推出原数列则被称为反演

$f(n)=\sum\limits_{i=n}^m{i\choose n}g(i)\Leftrightarrow g(n)=\sum\limits_{i=n}^m(-1)^{i-n}{i\choose n}f(i)$

证明: 见 参考中 的’反演’

快速计算

令 $a_i = (m−i)!g(m−i)$, $b_i = (m−i)!f(m−i)$

有

$a_j = (m-j)!g(m-j) $

$= \sum_{i=m-j}^m (-1)^{i-(m-j)} \frac{i!f(i)}{(i-(m-j))!} $

$= \sum_{i=0}^j (-1)^{(m-i)-(m-j)} \frac{(m-i)!f(m-i)}{((m-i)-(m-j))!} $

$= \sum_{i=0}^j \frac{(-1)^{j-i}}{(j-i)!}b_i$, 标准的$a_i = \sum b_j c_{i-j}$ 形式

一个fft, $O(n \log n)$搞定

注意到 $ e^{-x} = \sum \frac{(-1)^{i}}{i!}$

相当于生成方程 $a(x)=b(x)e^{-x}$, 注 这也是一种 反演推导可以用的路径

还有其它形式的二项式反演

$O(n^2)$ 解法

dp[i][j] = 排列P的前i个中, 有j个指定的 满足$P_k\ge B_k$ 的P的选择方案数, 对于未指定的位置可以满足也可以不满足

dp[i][j] = (N-Bi-(j-1)) dp[i-1][j-1](指定i) + dp[i-1][j] (不指定i), 注意到B非严格单调递减, 说明了前面消耗的P都比当前 Bi 大, 所以是N-Bi-(j-1)

G[L] = dp[N][L](N-L)!, 集合S 对应 L=|S| 每个满足的S 中固定的P[S[]] 对 dp[N][L] 贡献1, 对G[L] 贡献(N-L)!

这里 $N-Bi-(j-1)$ 可能为负数吗, 那应该对应0值? 还是允许负值,还是预先判断?

其实 这说明 >= Bi 的P的个数小于长度, 所以这种是无解的状态(方案数为0)

如果i-1的都正确计算了, 那么 显然 dp[i-1][j]=0

如果之前已经发生无解了, 那么dp[i-1][j-1] = 0 不受到系数影响(即如果系数是负数 会让前面转移的时候就已经是0,不会影响结果

如果之前有dp[i-1][j-1]的方案, 那么说明这里刚刚好不够了, 系数为0

所以始终可以直接使用这个值

$O(n \log^2 (n))$ 解法

令 $f[i][j] = dp[i][i-j], j \le i$, 因为$j > i$时全为0, 因为希望 转化成(Ci+j) * [j] + K*[j-1] 的形式,同时有$dp[i][j]=f[i][i-j]$

则 $f[i][j] = {dp}[i][i-j] $

$= (N-B_i-(i-j-1)){dp}[i-1][i-j-1]+ {dp}[i-1][i-j]$

$= (N-B_i-(i-j-1)){f}[i-1][j]+ {f}[i-1][j-1]$

$ = (N-B_i + 1 -i+ j){f}[i-1][j]+ {f}[i-1][j-1]$

令 $C_i = N-B_i+1-i$

$ = (C_i + j){f}[i-1][j]+ {f}[i-1][j-1]$, 题解这部分的-1有问题

考虑 $f_i(x)$为 $f[i]$ 的生成方程

有$f_i(x) = C_i f_ {i-1}(x) +xf’_ {i-1}(x) +xf_ {i-1}(x)=x(f_{i-1}(x)+f’_ {i-1}(x)) + C_i f_ {i-1}(x).$

$f_i(x)e^x = x(f_{i-1}(x)e^x+f’_ {i-1}(x)e^x) + C_i f_ {i-1}(x)e^x$

$f_i(x)e^x = x(f_{i-1}(x)e^x)’ + C_i f_ {i-1}(x)e^x$, 其实这里的想法就是 求导 看成系数左平移, 乘$x$看成右平移, 需要建立一个 平移量为0的等式, 同时第二项虽然 平移量 满足, 但是不是 fe^x形式, 这里看起来刚好

$\lbrack x^j \rbrack f_i(x)e^x = \lbrack x^j\rbrack (x(f_{i-1}(x)e^x)’ + C_i f_ {i-1}(x)e^x)$

令$g_{i} = f_i(x)e^x$,有系数$g_{i,j} = [x^j]f_i(x)e^x$

有系数关系$g_{i,j} = jg_{i-1,j} + C_i g_{i-1,j} = (j+C_i) g_{i-1,j} = g_{0,j} \prod_{k=1}^i (j+C_i)$

定义 $h(x) = \prod_{i=1}^N (x+C_i)$

这就是多项式多点求值

如果不变形dp

$dp[i][j] = (C_i-(j-1))dp[i-1][j-1] + dp[i-1][j]$

$f_i(x) = xC_i f_ {i-1}(x) -x^2f’_ {i-1}(x) +f_ {i-1}(x)$

$f_i(x)t_i(x) = xC_i f_ {i-1}(x)t_i(x) -x^2f’_ {i-1}(x)t_i(x) +f_ {i-1}(x)t_i(x)$

若 $f_i(x)t_i(x) = k_0 x(f_ {i-1}(x)t_{i-1}(x))’ + k_1f_ {i-1}(x)t_{i-1}(x)$

$k_0xt_{i-1}(x) = -x^2 t_{i}(x)$

$k_0xt_{i-1}’(x) + k_1t_{i-1}(x) = xC_it_{i}(x) + t_i(x)$

似乎没法搞, 所以可以看到 根本问题在于j 与 j-1 , j 的系数关系

只要形状是 $[j] = (C_i+k_0j)[j] + k_1[j-1]$的, <————– 这就是转化动机

就可以变成$f=C_if+k_0xf’ + k_1xf$, $\frac{k_1}{k_0}$ 是整数

$e^{\frac{k_1}{k_0}x}f=C_ie^{\frac{k_1}{k_0}x}f+k_0xe^{\frac{k_1}{k_0}x}f’ + k_1xe^{\frac{k_1}{k_0}x}f$

$e^{\frac{k_1}{k_0}x}f=C_ie^{\frac{k_1}{k_0}x}f+k_0x(e^{\frac{k_1}{k_0}x}f)’$

Multipoint evaluation 多项式多点求值

可以见37zigen写的, 更细节一些(日文)

给一个n次多项式 f(x), 和长m的整数序列 x

有办法在O(m log^2 m + n log n) 时间复杂度内算完 f(x1)…f(xm)

根据 多项式余数定理, f(a) = f(x) mod (x-a)

能算出 f(x) mod (x-xi)

分治思想, 考虑从叶子构造二叉树, 叶子(x-x1),(x-x2),(x-x3)….,(x-xn), 每个节点为它的两个叶子的乘积

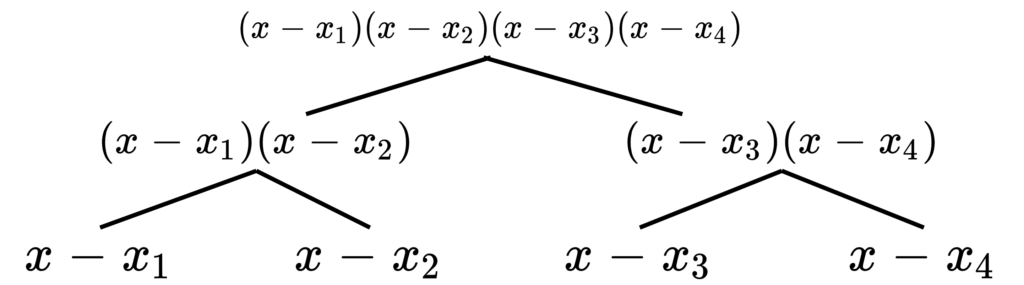
因为 f mod g = (f mod gh) mod g

所以计算 f mod (x-xi) 可以沿着二叉树 从根到叶子做mod

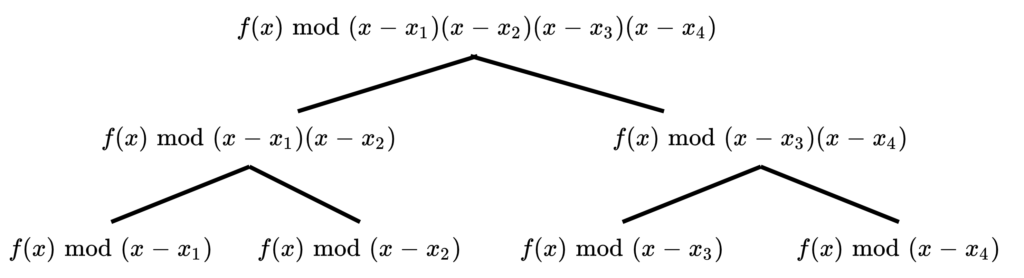
这样算的话 注意到每层 取模的 规模减半, 问题落在如何做多项式除法/取模

如果个数n不是2的幂次, 通过叶子补1, 把n补成2的幂次即可

所以对于 x1

f(x) = g(x)(x-x1) + (f(x) % (x-x1))

f(x1) = (f(x) % (x-x1))(x1)

注意到 (f(x) % (x-x1)) 其实是常数项

多项式 除法/模运算

$F(x)=G(x)Q(x)+R(x)$ 其中$R(x) = F(x) \mod G(x)$, F为n次, G为m次, 则Q(x)为 n-m次, R(x)不超过 m-1次

$F(\frac{1}{x})=G(\frac{1}{x})Q(\frac{1}{x})+R(\frac{1}{x})$, 同时乘上$x^n$

$x^n F(\frac{1}{x}) = x^m G(\frac{1}{x}) x^{n-m} Q(\frac{1}{x}) + x^{m-1} R(\frac{1}{x}) x^{n-m+1}$

这里如果$A(x)$是i次多项式 那么 $ x^i A(\frac{1}{x})$ 相当于对A做系数倒转

$rev(F)(x) = rev(G)(x)rev(Q)(x) + x^{n-m+1} rev(R)(x)$

$rev(F)(x) = rev(G)(x)rev(Q)(x) \pmod{x^{n-m+1}}$

$rev(Q)(x) = rev(F)(x) (rev(G)^{-1})(x) \pmod{x^{n-m+1}} $ 这里需要多项式 求逆

有了Q 的话, $R = F-GQ$ 也就很好求了

多项式 求逆

即$A(x) A^{-1}(x) \equiv 1 \pmod{x^n}$

若 $A(x)B(x) \equiv 1 \pmod{x^n}$, 有$A(x)B(x) \equiv 1 \pmod{x^{\lceil\frac{n}{2}\rceil}}$

若 $A(x)C(x) \equiv 1 \pmod{x^{\lceil \frac{n}{2} \rceil}}$ 有

$B(x)-C(x) \equiv 0 \pmod{x^{\lceil \frac{n}{2}\rceil}}$

$(B(x)-C(x))^2 \equiv 0 \pmod{x^n}$

$A(x)(B(x)-C(x))^2 \equiv 0 \pmod{x^n}$, 因为 所有小于n次项 至少由一个小于 $\lceil \frac{n}{2} \rceil$项构成,

$A(x)B(x)B(x)-2A(x)B(x)C(x)+A(x)C(x)C(x) \equiv 0 \pmod{x^n}$

$B(x)-2C(x)+A(x)C(x)C(x) \equiv 0 \pmod{x^n}$

$B(x)= C(x)(2-A(x)C(x)) \pmod{x^n}$

ftiasch

考虑 从0,0 走到 n,k 的路径方案数, 每次移动的方案数不是1, 而是上面dp的转移系数

编码调试

  1. $g_0 = f_0(x) e^x = 1\cdot e^x = e^x$, 因为$dp[0][0]=1, dp[0][>0] = 0$
  2. $h(x) = \prod_{i=1}^N (x+C_i) $,然后$h(0..N)$ 多项式多点求值, $C_i = N-B_i+1-i = N-(N-1-A_i)+1-i = A_i+2-i$
  3. $g_n[i] = g_0[i] h(i) 对应位置相乘$ for一遍 $O(N)$
  4. $f_n = g_n e^{-x}$ fft
  5. $G[L] = dp[n]\lbrack L \rbrack (N-L)! = f_n\lbrack n-L \rbrack L!$
  6. 二项式反演 $F(K) = \sum_{K\le L}(-1)^{L-K} \binom{L}{K} G(L)$
  7. 根据K 奇偶统计 得到概率, 概率 * n 就是期望

拿样例数据

1
2
2
0 1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
N=2

A[1]=0
A[2]=1

B[1]=1
B[2]=0

C[1]=1
C[2]=2

F(0)=0;
F(1)=1;
F(2)=1;

所以 ans = E = (F(0)+F(2))/n! * n = 1

G(0)+=binom(2,0) * F(2) + binom(1,0) * F(1) + binom(0,0) * F(0) = 2
G(1)+=binom(2,1) * F(2) + binom(1,1) * F(1) = 3
G(2)+=binom(2,2) * F(2) = 1

dp[i][j]:
  0 1 2 j
0 1 0 0
1 1 1 0 // (2-j)[j-1]+[j]
2 1 3 1 // (3-j)[j-1]+[j]
i

G(0)=2=1*2=dp[2][0](2-0)!
G(1)=3=3*1=dp[2][1](2-1)!
G(2)=1=1*1=dp[2][2](2-2)!

f[i][j]:
  0 1 2 j
0 1 0 0
1 1 1 0
2 1 3 1
i

g0(0)=1;
g0(1)=1;
g0(2)=1/2;

h(x)=(x+1)(x+1)=x^2+2x+1=(1,2,1)
h(0)=1
h(1)=4
h(2)=9

g2(0)=1*1=1
g2(1)=4*1=4
g2(2)=9*1/2=9/2

f2 = (1,3,1) = (1,4-1,1/2+9/2-4) = (1,4,9/2) x (1,-1,1/2) mod x^3

代码

人傻常数大 5765 Byte 4283ms

https://atcoder.jp/contests/abc272/submissions/35978028

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
#include <bits/stdc++.h>
#include <atcoder/modint>
#include <atcoder/convolution>
using mint = atcoder::modint998244353;
const int MOD=998244353;

namespace CMM{ // inv fac ifac binom
  template<class T,int MOD> // T should be modint
  class InvFacBinom{
    std::vector<T> _inv;
    int _n;
  public:
    std::vector<T> fac;
    std::vector<T> ifac; // invfac
    InvFacBinom(int n):_n(n){
      fac = std::vector<T> (n+1,1);
      _inv = std::vector<T> (n+1,1);
      ifac = std::vector<T> (n+1,1);
      for(int i=1;i<=n;i++) fac[i] = fac[i-1] * i;
      for(int i=2;i<=n;i++) _inv[i] = (MOD-MOD/i) * _inv[MOD%i];
      for(int i=1;i<=n;i++) ifac[i] = ifac[i-1] * _inv[i];
    }
  };
}


namespace CMM{
  template<class T>
    class Poly{
      std::vector<T>_d;
    public:
      Poly(const std::vector<T> &d):_d(d){};
      friend Poly operator+(const Poly&p0,const Poly&p1){
        std::vector<T>r=p0._d;
        if(p1._d.size()>r.size())r.resize(p1._d.size());
        for(int i=0;i<(int)p1._d.size();i++)r[i]+=p1._d[i];
        return r;
      }
      friend Poly operator-(const Poly&p0,const Poly&p1){
        std::vector<T>r=p0._d;
        if(p1._d.size()>r.size())r.resize(p1._d.size());
        for(int i=0;i<(int)p1._d.size();i++)r[i]-=p1._d[i];
        return r;
      }
      friend Poly operator*(const Poly&p0,const Poly&p1){ // ntt
        return atcoder::convolution(p0._d,p1._d);
      }
      std::vector<T> coef()const{
        return _d;
      }
      void Print() const{
        for(auto v:_d) printf("%d ",v.val());
        printf("\n");
      }
      template<int MOD>
        static Poly PolyEX(const InvFacBinom<T,MOD>&ifb,int n){ // e^x
          std::vector<T> p(n+1,0);
          for(int i=0;i<=n;i++)p[i]=ifb.ifac[i];
          return p;
        }
      template<int MOD>
        static Poly PolyENegX(const InvFacBinom<T,MOD>&ifb,int n){ // e^{-x}
          std::vector<T> p(n+1,0);
          for(int i=0;i<=n;i++)p[i]=ifb.ifac[i]*(i%2?-1:1);
          return p;
        }
      Poly Rev(int n) const{ // 颠倒[0..n]次的系数
        std::vector<T>r=_d;
        if(n+1>(int)r.size())r.resize(n+1);
        for(int i=0;i<(int)r.size()/2;i++)std::swap(r[i],r[r.size()-1-i]);
        return r;
      }
      Poly Modn(int n) const{ // return (this) mod x^n
        std::vector<T>r=_d;
        if((int)r.size()>n) r.resize(n);
        return r;
      }
      Poly Inv(int n) const{ // return this^{-1}, s.t. this this^{-1} \equiv 1 \pmod{x^n}
        assert(_d[0] != 0);
        Poly r = std::vector<T>{_d[0].inv()};
        for(int pwr=1;pwr<n;pwr*=2){
          r = r.Modn(pwr);
          r = r * (Poly({2}) - r * _d);
        }
        return r.Modn(n);
      }
      Poly Norm() const{ // 清除高位0
        std::vector<T>r=_d;
        while(r.size() > 1 && r.back()==0)r.pop_back();
        return r;
      }
      std::pair<Poly,Poly> Div(const Poly<T>& B) const{ // return  {A / B,A % B}
        const Poly& A=*this;
        int m=B._d.size()-1;
        int n=std::max(A._d.size()-1,B._d.size()-1); // n >= m
        // A=BC+D
        auto C=(A.Rev(n)*(B.Rev(m)).Inv(n-m+1)).Modn(n-m+1).Rev(n-m);
        auto D=(A-B*C).Norm();
        return {C,D};
      }
      std::vector<T> MPE(const std::vector<T>& a) const{ // Multipoint evaluation
        int sz=a.size();
        std::vector<std::vector<Poly > > tree = {{}};
        for(auto v:a)tree[0].push_back(std::vector<T>{-v,1}); // x-ai
        while((tree[0].size() & (tree[0].size()-1)))tree[0].push_back(std::vector<T>{1}); // 1
        while(tree.back().size() > 1){
          std::vector<Poly >row={};
          const auto&b=tree.back();
          for(int i=0;i<(int)b.size()/2;i++) row.push_back(b[i*2]*b[i*2+1]);
          tree.push_back(row);
        }
        std::vector<Poly > h = {Poly(_d)};
        // h[0] 表示 h, 从上向下取mod
        for(int i=tree.size()-1;i>=0;i--){
          std::vector<Poly > nexth = {};
          for(int j=0;j<(int)tree[i].size();j++) nexth.push_back(h[j/2].Div(tree[i][j]).second);
          h = nexth;
        }
        std::vector<T> res;
        for(int i=0;i<sz;i++) res.push_back(h[i]._d[0]);
        return res;
      }
    };
};

using namespace CMM;

// --------------- template ------------------

typedef long long ll;
#define rep(i,a,n) for (ll i=a;i<(ll)n;i++)
using poly=CMM::Poly<mint>;
std::vector<mint> G2F(const InvFacBinom<mint,MOD>& ifb, std::vector<mint> G){ // 二项式反演
  int n=G.size()-1; // 最高次
  std::vector<mint> b(n+1,0);
  rep(i,0,n+1) b[i]=ifb.fac[n-i]*G[n-i];
  auto a = (poly(b) * poly::PolyENegX<MOD>(ifb,n)).coef();
  std::vector<mint> F(n+1,0);
  rep(i,0,n+1)F[i]=a[n-i]*ifb.ifac[i];
  return F;
}

ll read(){ll r;scanf("%lld",&r);return r;}

int a[200010];
int c[200010]; // ci = n-bi+1-i = n-(n-1-ai)+1-i = ai+2-i

int main(){
  int n = read();
  InvFacBinom<mint,MOD> ifb(n);
  rep(i,1,n+1) a[i] = read();
  std::sort(a+1,a+n+1);
  rep(i,1,n+1) c[i] = a[i]+2-i;
  // --- init ----
  std::vector<poly> h={};
  rep(i,1,n+1) h.push_back(std::vector<mint>{c[i],1}); // h(x)=\prod (x+Ci)
  while(h.size()>1){// dc 分治
    std::vector<poly> newh={};
    rep(i,0,h.size()/2)newh.push_back(h[i*2]*h[i*2+1]);
    if(h.size()&1)newh.push_back(h.back());
    h=newh;
  }
  // h[0] 表示 h
  std::vector<mint> points(n+1);
  iota(points.begin(),points.end(),0); // [0..n]
  auto hi=h[0].MPE(points); // Multipoint evaluation
  auto g=poly::PolyEX<MOD>(ifb,n).coef(); // g0=f0e^x=1*e^x=e^x
  rep(i,0,n+1) g[i]*=hi[i];
  auto f = (poly(g)*poly::PolyENegX<MOD>(ifb,n)).coef(); // f= g*e^{-x}
  std::vector<mint> G(n+1,0);
  rep(i,0,n+1) G[i]=f[n-i]*ifb.fac[n-i];
  auto F=G2F(ifb,G);
  mint cnt=0;
  for(int i=2;i<=n;i+=2) cnt += F[i];
  printf("%d\n",(cnt*ifb.ifac[n-1]).val()); 
  return 0;
}

总结

G

靠概率的不打算学了

crying这个相邻的性质应该很明显啊,我自己咋就想不到

有想到说可以排序, 但没想到排序能带来什么好处, 这里看起来是 相邻的差的和小于最大最小的差, 这样让sqrt的质因数分解总的代价也不会过大

Ex

这里问题转化的部分其实做到了

看来是容斥原理完全不会了, 在不往后看得话, 我也没有直观的直觉,觉得G更好算,我考虑的容斥 在想能否一步到一个明显好算的但没想出

参考

官方题解

洛谷 P5050 模版 多项式多点求值

oi wiki 多项式取模

  • 多项式多点求值

https://37zigen.com/multipoint-evaluation/

https://rsk0315.hatenablog.com/entry/2020/04/05/190941

  • Hakone Ekiden DP

https://judge.u-aizu.ac.jp/onlinejudge/description.jsp?id=2439&lang=jp

https://atcoder.jp/contests/abc134/tasks/abc134_f

反演