Atcoder abc250

發表於 更新於 分類於 ， Disqus： 文章字數： 2.8k 所需閱讀時間 ≈ 9 分鐘
F(计算几何,滑窗)G(贪心)Ex(最小生成树)

https://atcoder.jp/contests/abc250/tasks

F - One Fourth

平面凸n边形

选非相邻点切割

求min( 8 abs(size/4 - eated))

就是选一些点, 围成的凸多边形 min(8abs(size * 3/4 - 选定凸多边形 ))

只切一次!!!!!!!!!!!!!!!!!!!!

范围

n 1e5

x,y [-4e8,4e8]

2s

1024 mb

我的思路

没做过多少计算几何相关的题目

一个想法是, 假设一个点会被保留, 想做前i个点, 第i个点保留的 最大, 小于目标的面积, 但似乎没有局部性

因为看起来像有相互冲突的背包

如果不是1/4, 是1/2呢, 我似乎1/2也不会做

干,读错题, 只切一次………….

题解

一个n^2 的方法

选点i, 移动j=i+1…

然后算大小, 每次增加被切三角形的面积

加个滑窗双指针就没了

代码

https://atcoder.jp/contests/abc250/submissions/35189253

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
#include <bits/stdc++.h>
using namespace std;

typedef long long ll;
#define rep(i,a,n) for (ll i=a;i<(ll)n;i++)
ll read(){ll r;scanf("%lld",&r);return r;}

int n;

vector<pair<ll,ll> > p;

ll cross(const pair<ll,ll>& a0,const pair<ll,ll>&a1){ // = area * 2
  return a0.first*a1.second - a1.first * a0.second;
}
// p0 - p1
pair<ll,ll> sub(const pair<ll,ll> &p0,const pair<ll,ll>&p1){
  return {p0.first - p1.first,p0.second-p1.second};
}

ll S(const pair<ll,ll> &p0,const pair<ll,ll>&p1,const pair<ll,ll>&p2){
  return cross(sub(p1,p0),sub(p2,p0));
}


int main(){
  int n = read(); // N 1e5
  rep(i,0,n) p.push_back({read(),read()});
  auto o = p[0];
  sort(p.begin()+1,p.end(),[=](auto p0,auto p1){
      return cross(sub(p0,o),sub(p1,o)) > 0;
  });
  ll s = 0;
  rep(i,1,n-1) s += S(o,p[i],p[i+1]);

  int i = 0;
  int j = i+1;
  ll ans = 0x3f3f3f3f3f3f3f3f;
  ll area = 0;
  do{
    while(area*4 < s && (j+1)%n != i){
      area += S(p[i],p[j],p[(j+1)%n]);
      ans = min(ans, abs(s-4*area));
      (j+=1)%=n;
    }
    area -= S(p[i],p[(i+1)%n],p[j]);
    ans = min(ans, abs(s-4*area));
    (i+=1)%=n;
  }while(i!=0);
  printf("%lld\n",ans);
  return 0;
}

G - Stonks

n天, 第i天 pi

每天 可以 买1单位/卖1单位

足够多初始金钱

求最大赚的数量

范围

n 2e5

pi [1,1e9]

2s

1024mb

我的思路

显然买的次数=卖的次数

如果只有一买卖次, 那么就是维护前缀最低, ans=max(ans, 当前-前缀min)

考虑两次

如果两次的操作与第一次最优的方案都没有重叠

那么其中一组用第一次的替换不会更差

所以两次的方案, 中出现一次的操作相关的也可以得到最优答案

但是并不好拆

一个复杂度明显会超的dp是

dp[i][j] = 前i个, 持有j个

转移dp[i][j] = max(dp[i-1][j], j>0 && dp[i-1][j-1]-a[i],dp[i-1][j+1]+a[i])

最后答案 = dp[i][0]

再就是, 作为卖的价格, 都是尽量选大的, 而买的价格都是尽量小的

有没有可能 从值考虑去看范围

但是例如 3 4 1 2, 就会出现有的买比卖还大

然后就是能不能贪心

每次获得最大的

然后在这个前面中找最小的, 做成一对产生收益, 都删掉

如此重复?

这样的话, 线段树一类可以维护+查询

问题是是否有正确性

1 3 2 4, 显然能产生代价为4, 而不是3

考虑剩下的未被选的

显然是一个单调递减的序列

考虑说前i-1个如果通过了两两配对达到了最大, 那么剩余的就是一个单调递减序列

现在多一个a[i] 对答案会有什么影响

3 1 2 4, 最大是3

再一个就是 上面可以看到 就是给一个前缀和 >= 0 的 1/0/-1序列和 a[i]的乘积最大

题解

也是上来, 和我一样的一个n^2 dp

然后说把dp看成二维表, 考虑 做一些列上的处理

例如输入

1
2
8
2 5 4 3 7 1 8 6

会有

1
2
3
4
5
6
7
8
 0  -2
 3  -2  -7
 3  -1  -6 -11
 3   0  -4  -9 -14
 7   3  -2  -7 -14 -21
 7   6   2  -3  -8 -15 -22
14  10   5   0  -7 -14 -22 -30
16  11   6   0  -6 -13 -20 -28 -36

做dp[i][j-1]-dp[i][j], 有

1
2
3
4
5
6
7
8
2
5 5
4 5 5
3 4 5 5
4 5 5 7 7
1 4 5 5 7 7
4 5 5 7 7 8 8
5 5 6 6 7 7 8 8

题解要我观察, 我啥都没观察出, 只看出这些数都是来自 输入的元素

记录所有可以贡献的点

那么增加a[i],找最小的小于a[i] 可连接的, 如果前面

如果是没匹配的,y < a[i], 则(y,a[i]) 构成一对

x < y < a[i]

那么, (x,a[i]) 成一组, y单独 拎出来 等待匹配, 而两种做法, a[i] 都是未来可以匹配的

所以如果一个点z成为卖出, 那它还可以成为两次买入, (x,y) + z = (x,z) + y => (x,?) +z => (z,!)

如果一个点没有成为卖出,那它还可以成为 一次 买入

proof

横坐标j, 纵坐标dp[i][j] 画曲线

考虑dp[i]的曲线 如何变到dp[i+1]的曲线

注意到上面的转移方程dp[i][j] = max(dp[i-1][j],dp[i-1][j-1]-A[i],dp[i-1][j+1]+A[i])

黑色为dp[6], 蓝色为 max第二项, 红色为max第三项

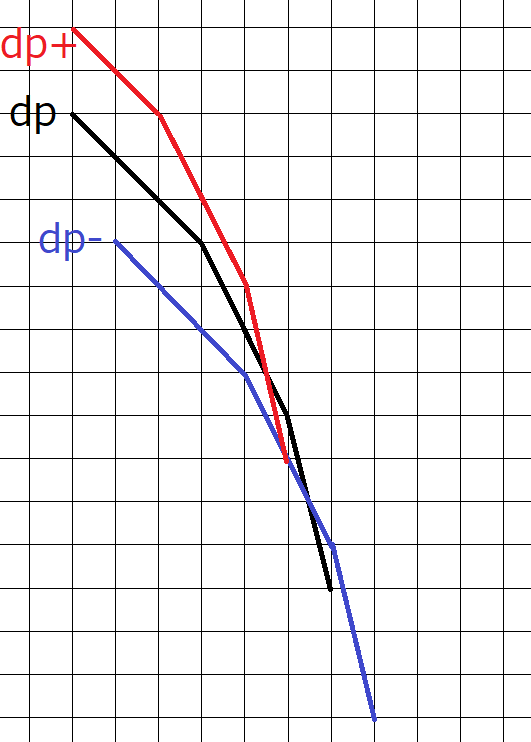
然后证明, dp和dp+, 一部分是dp大一部分是dp+大, dp和dp-也是, 且结果还是上凸

并且分割的位置,就是 斜率 -a[i] 处

???????? 没看懂这说的和上面的操作之间的关系, 怎么就证明了

代码

https://atcoder.jp/contests/abc250/submissions/35191923

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
ll read(){ll r;scanf("%lld",&r);return r;} // read

priority_queue<ll,vector<ll>,greater<ll>>q; // 小根堆

int main() {
  int n = read();
  ll ans=0;
  while(n--){
    ll x=read();
    if(!q.empty()&&q.top()<x){
      ans+=x-q.top();
      q.pop();
      q.push(x);
    }
    q.push(x);
  }
  printf("%lld\n",ans);
}

Ex - Trespassing Takahashi

n 个点, m 边的路, 第i条需要ci分钟, 连通图

其中k个点是可以休息的

对于q个询问,ti从小到大

从任意可休息点移动时间不能超过ti, 到达任意一个休息点后把累计移动时间清零, 问他能否从休息点xi开始走到达休息点yi

范围

k,n 2e5

m 2e5

ci [1,1e9]

q 2e5

ti 1e15

7s

1024mb

我的思路

对于不同的Q来说, 有xi,yi,ti 3个变量

ti既然给的就是从小到大,那么休息点之间的并查集关系也是逐渐合并的

一个TLE的方法是

求休息点之间的距离建立并查集, 然后看xi和yi是否同一个并查集

问题是, 难以低复杂度求两两之间的最短距离,

题解

也是一样考虑k个点的图G,两两之间是距离, 然后上并查集 需要 O(k^2)

优化

假设T是G的最小生成树, 那么T的答案和G等价

proof

显然最小生成树过程中 都是将两个不同的连通块连在一起,用当前可用的最短边, 所以现在问题是<=ti的边能否把一些点连成同一个连通块,

当<=ti让u和v不在同一个连通块时, 显然最小生成树上u到v的路径也有> ti的边,

而当<=ti让u和v在同一连通块时,

对<=ti的边染色为黑色, > ti的边染色为白色

重新考虑T的生成过程, 如果有任意黑色边能让两个不连通的块连通之前,不会选任何白色, 因此在选白色之前, u和v就已经连通了,所以最小生成树上问题等价

以上证明了只需要k-1条边, 但如何找呢

Borůvka 算法, 相当于 多源Prim

对于现在的每个连通块，找到从这个连通块出发，不在最小生成树中的、到达别的连通块的最短边。(相等的边增加额外顺序, 避免A-1-B-1-C-1-A这种形成环,也可以并查集保护)

把这些边全部加入最小生成树中

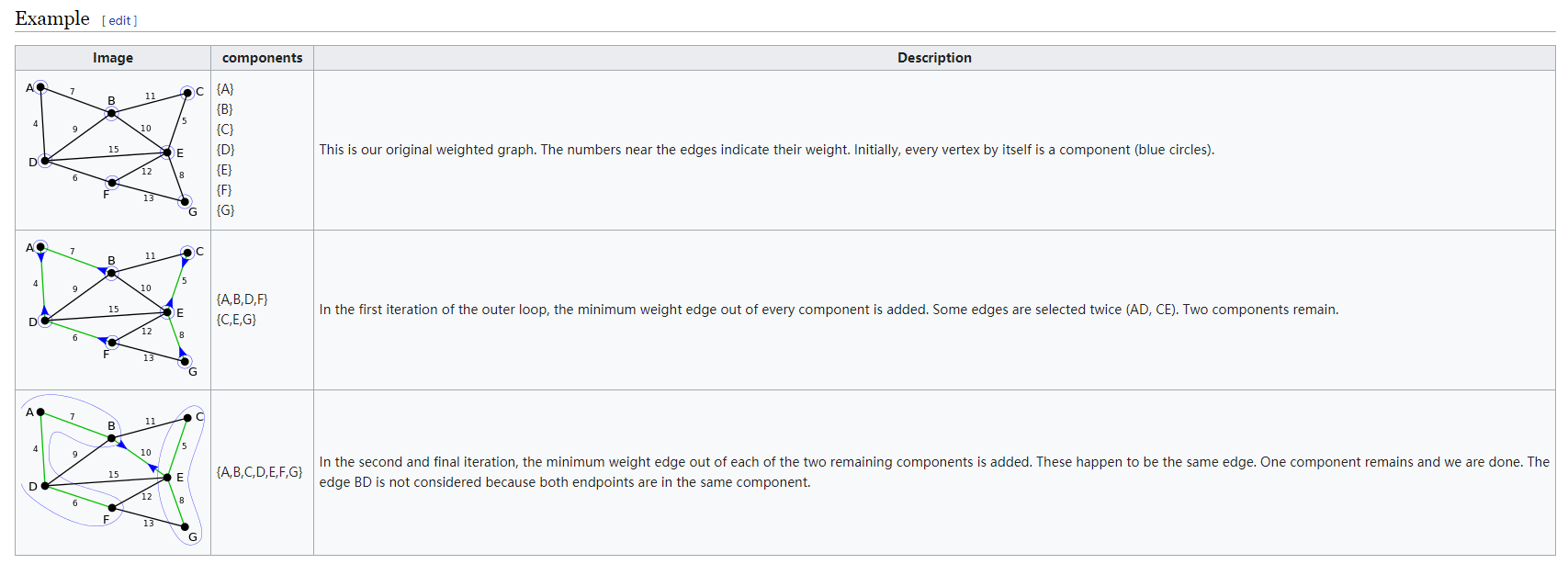
每次O(M) 但是每次联通块个数减半, 所以O(ElogV)

另一个方法

u-a-b-v

= (u-a-b)-(v)

可以由 (u-..-a)的最短 +(a-b) + (b-..-v)的最短

然后所有休息点做多源 dij

计算每个点 到 最近的休息点的 距离和是哪个点

a-1-?-2-b, ?-3-c 的话,不会计算b-c的距离, 只会计算

a-b: (a-?)+(?-b)+(b-b)

a-c: (a-?)+(?-c)+(c-c)

proof

这个相当于是从边是否经过的角度考虑

如果经过边i, 当前限制为t, 如果 ci+ d[a_i]+d[b_i] > t (也就是经过这个边的最近的两个点都超过t) 那么这个边一定不经过

否则 链接 最近的两个点

又两个d至少一个小于t/2

所以对于一侧来讲,归纳显然相当于一侧全连通(因为只关心并查集关系,不关系具体边)

例如t=15, 那么a的一侧一定全连通

a'-1-a-1-b-10-b'

而对于右侧 a'-1-a-1-b-11-b''

向这种, 那么就是取b-…-b’’ 路径上的边 b-?

要么是(a’-b) + (b-?) + (?-b’’)

要么是(b’-b) + (b-?) + (?-b’’)

因为b的最近点只可能是a’或者b’, 所以如果合法依然连通

得证

这样找的距离 产生的图, 的<=t的联通性不变

代码

https://atcoder.jp/contests/abc250/submissions/35205404

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define rep(i,a,n) for (ll i=a;i<(ll)n;i++)
ll read(){ll r;scanf("%lld",&r);return r;}
template <typename T> using minPQ = priority_queue<T,vector<T>, greater<T>>;

vector<pair<int,ll> > g[200010]; // g[u] = {v,w};
int fa[200010]; // DSU
int find(int v){return v==fa[v]?v:(fa[v]=find(fa[v]));}
const ll INF = 0x3f3f3f3f3f3f3f3f;
int main() {
  int n = read();
  int m = read();
  int k = read();

  vector<tuple<ll,int,int> > e; // w,u,v 原图的边
  rep(i,0,m){
    int u = read()-1; // 0-index
    int v = read()-1;
    ll w = read();
    e.push_back({w,u,v});
    g[u].push_back({v, w});
    g[v].push_back({u, w});
  }

  vector<ll> h(n);     // 最近休息点
  vector<ll> d(n,INF); // 到最近休息点的距离
  minPQ<tuple<ll,int,int> > pq; // {dis, u, 休息点}
  rep(i,0,k) pq.push({0,i,i});
  for(int cnt = n;!pq.empty() && cnt > 0;) {
    auto [c,u,x] = pq.top();
    pq.pop();
    if (d[u]!=INF) continue;
    d[u] = c;
    h[u] = x;
    cnt --;
    for(auto [v,w]:g[u])if(d[v]==INF)pq.push({c+w,v,x});
  }

  vector<tuple<ll,int,int> > e2; // w u v, 只有k个点的图的边
  for(auto [w,u,v]:e) if(h[u] != h[v]) e2.push_back({d[u]+d[v]+w,h[u], h[v]}); // h[u]..u..v..h[v]
  sort(e2.begin(), e2.end());
  iota(fa,fa+k,0);

  int q = read();
  int i = 0;
  while(q--){
    int x = read()-1;
    int y = read()-1;
    ll t = read();
    while(i<(int)e2.size()){
      auto [w,u,v] = e2[i];
      if(w > t)break;
      fa[find(u)] = find(v);
      i++;
    }
    printf("%s\n",find(x)==find(y) ? "Yes" : "No");
  }
}

总结

F

不要读错题,不要读错题,不要读错题,不要读错题,不要读错题

还是先考虑多项式暴力方法再转换, 然后就滑窗呗

G

贪心也感觉没证明, 证明也没看懂有啥关系

Ex

最小生成树 一般都写的Kursukal,基本没写过Prim(一个点开始不断贪心扩最短边), 更不要说 Borůvka’s

这个 u-a-b-v 的想法, 感觉有点像找直径时候的中间的点的想法, 这<= t的连通性 等价证明

参考

官方题解

洛谷 Borůvka