Atcoder abc243

發表於 更新於 分類於 ， Disqus： 文章字數： 1.9k 所需閱讀時間 ≈ 6 分鐘
Ex(数学,bfs,DP)

https://atcoder.jp/contests/abc243/tasks

Ex - Builder Takahashi (Enhanced version)

给定S,G,O,. 组成的高h,宽w的矩阵, 其中S和G分别出现且仅出现一次

S起点

G终点

.可以建墙

O不可建墙

四临移动

问

  1. 最少建立多少墙可以让无法从S到G
  2. 满足最少墙时的方案数 mod 998244353

范围

h [2,100]

w [2,100]

4s

1024mb

我的思路

首先想到的是 直接建一个竖着或这横着的, 这样隔开就行了

又想到, 直接把起点或者终点围起来

那么问题就是能不能围住

那么先不管多少, 就把所有能建的全建立完, 那能走的只有4临可达的不能建的

所以判断能否很好判断

那么就是 最小代价的围

感觉不会超过100

但想了下要是能建立的是个蛇形, 那还是会很长接近平方

反正问题变成平面上一堆4临连在一起的S, 和一堆4临连在一起的G

要画圈/线 把两堆隔开, 然后有些不能画线的地方

1
2
3
4
5
6
7

  sss
    s
xxx s
    s
  sss

注意到虽然 不能画的x与s不相连, 但是依然可能影响围住s的大小

没啥想法, 感觉直接围起来 保证不了最小

1
2
3
4
5
6
7
8
9

sss
s
s
sss
s
s
sss

如果围完以后, 找 两点最短更新,需要保证包裹住

需要A星 一类的启发式吗?

但如果上了启发 后面统计又不太行了

甚至可能包裹和 隔断等价

1
2
3
4
5
6
           g
           g
ss         g
ss         g
           g
           g

没有头绪

题解

还是说 需要找个8临路径/环 把其中一个框起来

然后是如何操作

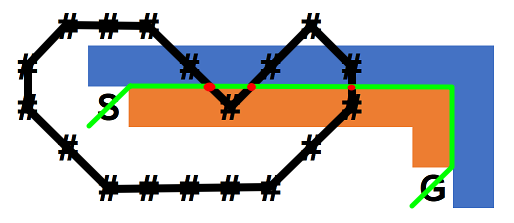
先任意找一条S到G的路径, 图中橙色

然后考虑路径上方可达的方块集合, 蓝色

井号是一个建立墙的方案(还没有考虑最小

一个有效分割方案 是 墙的线 跨过 橙色/蓝色的分界处奇数次!!!!!, 上面途中是3次

神奇 , 这是离散状态下的跨过!!

因为如果是非离散的, 其实就是两点之间的连线, 如果不重叠不相切, 那么就是交点为奇数个

而这里是离散的路径,所以通过两个贴在一起的有效路径, 其拼接的地方就可以看成线, 跨过就是一个交点

abc243Ex

然后 变成最短路问题?

因为连接的路径至少要被断开一个

那么遍历橙色上的点(x,y),对于给定的(x,y)

dp[i,j,f] = {从(x,y)出发走到(i,j,穿过线的次数奇偶性为f)的最短路的长度, 方案数}

然后 ans= d[x,y,1]

两个问题

是如何保证没有重复的走过的位置?

虽然如果一个走的序列有重复, ....x...x..., 可以把中间的....x去掉, 是这里有奇偶性, 直接去掉是不合逻辑的

假设中间这一段是偶数次穿过, 那么显然可以去掉 总的奇偶不变 路径更短, 因此可去掉

假设中间这一段是奇数次穿过, 那么不能去掉, 但是这一段就是一个解, 比整个短, 所以虽然不能去,但这个方案肯定不是最短 方案,也不影响答案

不同的x,y选择时之间怎么保证没有重复统计?

1
2
3
4
         ###
.       #sOO??
         ##OOO#         tOOOOOOOOOOOO
           ###

比如图中的两个问号?可能同时选为#

那么用一个方案中经过的最小橙色作为标识, 也就是 在计算时把前面的橙色置为不可放置就行了

坑

wa x 3

https://atcoder.jp/contests/abc243/submissions/36080360

问题在于不是圈是 拼的边怎么算

我把外面的 看作一个特殊点 大圈, 但是下面这种会重复统计.-. 和 .-外-.

1
2
3
4
5
4 6
OG..OO
O.SO.O
OO..OO
OOOOOO

然后直接考虑边界到边界, 注意重复处理, 两个点相邻且不跨色时 只统计一次, 不相邻的两个边界点或者相邻但是跨色的, 可以 通过边界完成不跨色

代码

https://atcoder.jp/contests/abc243/submissions/36080884

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
#include <bits/stdc++.h>
#include <atcoder/modint>
using mint = atcoder::modint998244353;
using namespace std;
#define rep(i,a,n) for (int i=a;i<(int)n;i++)
int read(){int r;scanf("%d",&r);return r;}
// Ex
int n,m;
const int INF=0x3f3f3f3f;
char s[110][110];
const int di[]={0,0,1,-1,1,1,-1,-1};
const int dj[]={1,-1,0,0,-1,1,-1,1};
bool dot(int i,int j){return i>=0&&i<n&&j>=0&&j<m&&s[i][j]=='.';} // only dot
bool border(int i,int j){return (i==0||i+1==n||j==0||j+1==m)&&s[i][j]=='.';} // only dot
vector<pair<int,int>>bs;// point on border maynot `.`

template<class T>
pair<int,mint> solve(int si,int sj,T&c0,T&c1){ // 除了环 还有边界到边界
  auto dp=vector(n,vector(m,vector<pair<int,mint>>(2,{INF,0}))); // len, ways
  vector<tuple<int,int,int,int>>bfs={};
  auto add=[&](int i,int j,int t,int l,mint w){
    auto&[tl,tw]=dp[i][j][t];
    if(tl==l) tw+=w;
    else if(tl > l){
      tl=l;
      tw=w;
      bfs.push_back({i,j,t,l});
    }
  };
  add(si,sj,0,0,1);
  rep(i,0,bfs.size()){
    auto [pi,pj,t,l]=bfs[i];
    auto [l1,w]=dp[pi][pj][t];
    assert(l==l1);
    assert(dot(pi,pj));
    auto cross=[&](int i0,int j0,int i1,int j1){ // 跨过颜色
      return (c0[i0][j0]&&c1[i1][j1]) || (c1[i0][j0]&&c0[i1][j1]);
    };
    rep(k,0,8){
      int ni=pi+di[k]; // (pi,pj) -> (ni,nj)
      int nj=pj+dj[k];
      if(!dot(ni,nj))continue;
      int nt=t^cross(pi,pj,ni,nj);
      add(ni,nj,nt,l+1,w);
    }
    if(border(pi,pj)) for(auto [ni,nj]:bs)if(border(ni,nj)) if(ni!=pi||nj!=pj){ // 线border<->border
      if(abs(pi-ni)<=1&&abs(pj-nj)<=1 && !cross(pi,pj,ni,nj))continue; // 8邻且未跨颜色, 则不要重复统计
      add(ni,nj,t,l+1,w);
    }
  }
  return dp[si][sj][1]; // 圈
}

int main(){
  n=read();
  m=read();
  rep(i,0,n)scanf("%s",s[i]);
  pair<int,int>S;
  pair<int,int>G;
  rep(i,0,n)rep(j,0,m) if(s[i][j]=='S') S={i,j};
  rep(i,0,n)rep(j,0,m) if(s[i][j]=='G') G={i,j};
  if(S>G)swap(S,G);
  auto [si,sj]=S;
  auto [gi,gj]=G;
  s[si][sj]='S';
  s[gi][gj]='G';
  if(sj > gj){
    rep(i,0,n) rep(j,0,m/2) swap(s[i][j],s[i][m-1-j]);
    rep(i,0,n)rep(j,0,m) if(s[i][j]=='S') S={i,j};
    rep(i,0,n)rep(j,0,m) if(s[i][j]=='G') G={i,j};
    tie(si,sj) = S;
    tie(gi,gj) = G;
  }
  assert(si<=gi && sj<=gj);
  rep(i,0,n)rep(j,0,m)if(border(i,j))bs.push_back({i,j});
  // ---
  auto c0=vector(n+1,vector(m,false)); // color 0
  auto c1=vector(n+1,vector(m,false)); // color 1
  auto addline=[](auto&arr,pair<int,int>S,pair<int,int>G){
    auto [si,sj]=S;
    auto [gi,gj]=G;
    assert(si==gi || sj==gj);
    if(si==gi) rep(j,min(sj,gj),max(sj,gj)+1) arr[si][j]=true;
    else       rep(i,min(si,gi),max(si,gi)+1) arr[i][sj]=true;
  };
  if(si == gi) {
    addline(c0,S,G);
    if(si==0) addline(c1,{1   ,sj},{1   ,gj}); // 注意不要出界
    else      addline(c1,{si-1,sj},{gi-1,gj});
  }else if(sj==gj){ // si < gi
    addline(c0,S,G);
    if(sj==0) addline(c1,{si,   1},{gi,   1}); // 注意不要出界
    else      addline(c1,{si,sj-1},{gi,gj-1});
  }else{ // si < gi && sj < gj
    addline(c0,S,{gi,sj});
    addline(c0,  {gi,sj},G);
    addline(c1,{si,sj+1},{gi-1,sj+1});
    addline(c1,          {gi-1,sj+1},{gi-1,gj});
  }
  int len=INF;
  mint cnt=0;
  rep(i,0,n)rep(j,0,m)if(dot(i,j)&&c0[i][j]){
    auto [sz,c]=solve(i,j,c0,c1);
    s[i][j]='O'; // 置为不可放避免重复统计
    if(sz==len){
      cnt+=c;
    }else if(sz<len){
      len=sz;
      cnt=c;
    }
  }
  if(len==INF){
    printf("No\n");
  }else{
    printf("Yes\n");
    printf("%d %d\n",len ,(cnt/2).val()); // 环会被正向和反向各统计一次
    return 0;
  }
}

总结

Ex

离散下的线交点

然后 这个环的个数也很神奇, 因为就算给了我这样构建图, 我虽然能想到这样的dp方向, 但是重复点的问题 直接想不出,只有给出了然后去证明

参考

官方题解