project_selection_problem
TLDR
有依赖关系的选择的问题,可以转化成 图论的最小割问题,再黑盒性质使用 最小割=最大流求出
project selection problem
https://codeforces.com/blog/entry/101354
流问题是算法竞赛的一个高级课题。 流问题的主要挑战往往不在于算法本身,而在于图的建模。 为了解决Project Selection Problem,我们将把它建模为最小切割问题的一个实例:”给你一个带加权边的有向图。 一个节点被指定为源节点,另一个节点被指定为汇节点。 删除一组总重量最小的边,使源点和汇点断开。 如果源点和汇点之间不再存在有向路径,则视为断开。 请注意,我们可以将最大流量问题视为一个黑盒子,它可以解决我们的最小切割问题。 因此,一旦我们设法将问题简化为最小切割,我们就可以认为问题已经解决。
Project Selection Problem 常见的形式
给定 N 项目 和 M个 机器,
第$i$个机器代价$q_i$
第$i$个项目产生$p_i$个收入
每个项目需要一组机器
如果多个项目 需要同样的一组机器, 他们共享这些机器
要求 $\max(\sum \mathrm{revenues} - \sum \mathrm{costs})$
对于项目来说,我们可以获得收入,而对于机器来说,我们必须支付费用,这很不方便,因此我们假定,我们为项目预付了费用,如果我们不能完成项目,就必须把钱退还给我们。 这两种方案显然是等价的,但后者更容易建模。
将上述问题建模为最小切割的一个简单方法是创建一个具有 N+M+2 个顶点的图。 每个顶点代表源、汇、项目或机器。 我们用 S 表示源,用 T 表示汇,用 $P_i$ 表示第 i 个项目,用 $M_i$ 表示第 $i$ 个机器。 然后,在源S和第 i 项目之间添加权重为 $p_i$ 的边,在第 i 机器和汇T之间添加权重为 $q_i$ 的边,在每个项目和其所需的每台机器之间添加权重为 ∞ 的边。
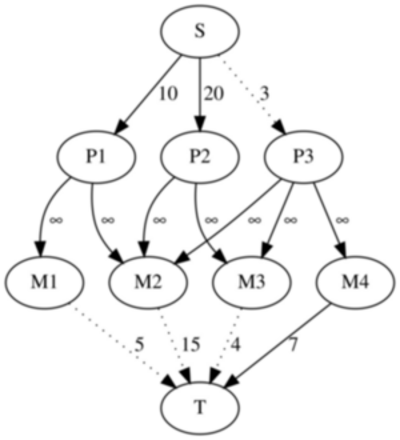
看三个边的意义,首先最明显的反而是无穷的边,因为P和M的依赖关系,建立的无穷边,所以说明了它们之间不会割,从而要么是和S切断,要么是和T切断
例如这里
- P1->m1m2和T切断
- P2->m2m3和T切断
- P3->m2m3m4 和S切断
要求的结果是最大价值 = sum(选择p)-sum(选择m)
而图论里是求最小割,所以 = sum 所有p - sum(未选择p)-sum(选择m) = sum 所有p - min(sum(未选择p)+sum(选择m))
所以
- 这里
S->P的割要表示 不选择P - 这里
M->T的割要表示 选择M
所有S->T的路径都是 S->P->M->T
所以 每个路径要么不选择P,要么选择M 逻辑上等价
我们的模型甚至可以扩展到 2 个项目之间或 2 台机器之间的依赖关系。 例如,假设项目 i 依赖于项目 j。 为了表示这一限制,我们可以在 i 到 j 之间添加一条权重为 ∞ 的边。 实质上,这条边告诉我们,如果不放弃项目 i ,就不能放弃项目 j 。 如果机器 i 依赖于机器 j ,我们就必须在图中添加一条从机器 i 到机器 j的边。 我们甚至可以在机器和项目之间添加依赖关系。 由此不难看出,机器和项目之间除了成本之外其实并无区别,从本质上说,机器只是一个需要花钱的项目。
最后一个细节是,在时间悖论的情况下,例如项目 1 需要项目 2 ,项目 2 需要项目 3 ,项目 3 需要项目 1,我们可以使用我们的模型意外地把它们都拿走。 如果没有问题,那就没有问题。 否则,如果项目应该按顺序进行,而不是一次性完成,我们就必须从图中删除所有属于循环的节点。
项目选择问题可以以多种形式出现。 例如,机器和项目也可以表示为衣服和服装或其他类比。 在这种情况下,我们可以很容易地识别出与原始问题之间的联系,并极快地制定出解决方案。 然而,”机器和项目 “往往不是用简单的物体来表示,而是用更抽象的概念来表示。
The Closure Problem
给你一个有向图。 每个节点都有一定的权重。 我们将闭包定义为这样一组节点:不存在从闭包内部指向闭包外部的边。 找出权重之和最大的闭包。
上述问题在民间被称为闭合问题。 封闭性要求可重新表述如下。 对于每条边 (x,y) 如果 x 在闭合中,那么 y 也必须包含在闭合中。
不难看出,这个问题与项目选择问题密切相关,甚至是等价的。 我们可以将节点包含在闭包中作为一个 “项目 “来建模。 这些限制也可以很容易地模拟为项目之间的依赖关系。 需要注意的是,在这种情况下,机器和项目之间并没有明确的界限。
This problem can also be disguised as open-pit mining. Once again, it is easy to see the connection between these 22 problems. Here is a sample submission implementing this idea.
一个更抽象的例子 A more abstract example
给你一个带有加权节点和加权边的图形。 请选择权重最大的节点和边的有效子集。 如果每个包含的边的两个端点也包含在子集中,则该子集被认为是有效的
我们可以把节点看作 “机器”,把边看作项目。 现在,我们不难发现,一条边依赖于它的 2 个端点,就相当于一个项目依赖于 2 台机器。
This problem can be found here and a sample submission can be found here. If we didn’t know about the project selection problem, then this problem would have been much harder.
An even more abstract example
您计划在一条街道上建造房屋。 街道上有 n 个可建房屋的位置。 这些位置从左到右依次为 1 到 N 。 在每个点上,你都可以建造一座高度在 0 和 H 之间的整数房屋。
在每个点上,如果房子的高度为 a,你可以从中获得 $a^2$ 美元。
虽然该市有 M 分区限制。 第 i 项限制规定,如果从 li 到 ri 处最高的房屋严格超过 xi ,则必须缴纳 ci 的罚款。
您想建造房屋,以获得最大利润(获得的美元减去罚款的总和)。 请确定可能的最大利润。
让我们重新表述一下限制条件。 对于限制条件(li,ri,xi,ci),我们可以假定我们会因为所有这些限制条件而受到惩罚(先全部受罚),并且如果我们在 [li,ri] 都小于或等于 xi 则会拿回ci 。 通过这个小修改,我们现在只能获得货币收益。
假设最大高度为 H 。 假设最初所有建筑物的高度都是 H ,并且有多个项目可以降低高度。 例如,(i,h) 代表将第 i 座从高度 h 降低到 h-1 ,成本为 $h^2-(h-1)^2$。 项目 (i,h) 显然取决于项目 (i,h+1) 。 让我们把限制条件也作为项目加入。 限制条件(li,ri,xi,ci)等同于一个项目,其利润 ci 取决于项目 (li,xi), (li+1,xi) … (ri,xi) 。 用不太正式的话来说,这意味着如果我们将第 li , li+1 …… ri 建筑物的高度降低到 hi,我们就可以重新获得资金。
请注意,这个问题也可以用动态编程法来解决。 不过,我们的解决方案有一个最大的优点,那就是更容易推广。 例如,我们可以很容易地修改这一方案,以考虑对一组非连续建筑物的限制。
This problem can be found here and a sample submission implementing this idea can be found here. The editorial of this problem also describes another approach using maximum flow, that is more or less equivalent to the one presented here.
Conclusion
项目选择问题是模拟问题时的一个有用工具。 当然,这些问题也可以直接用最大流量问题来模拟,但使用这种已有的方法更为简便。