D
https://codeforces.com/contest/1677/problem/D
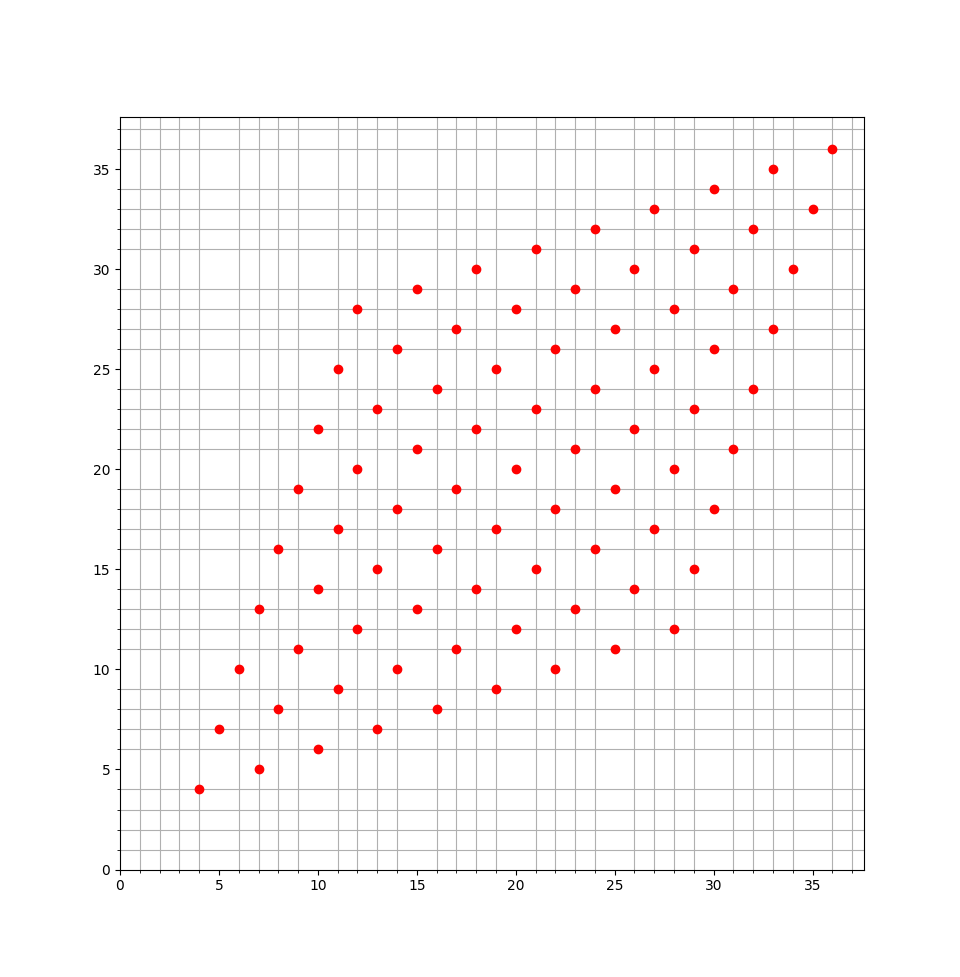
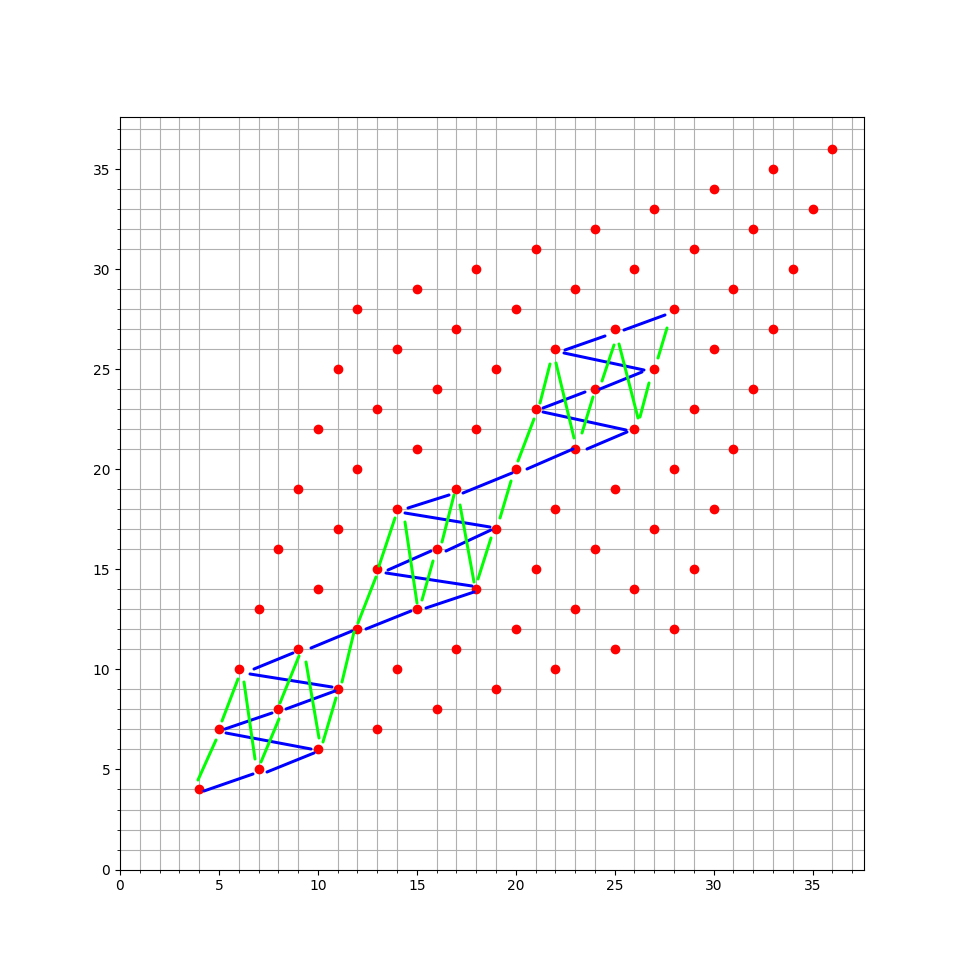
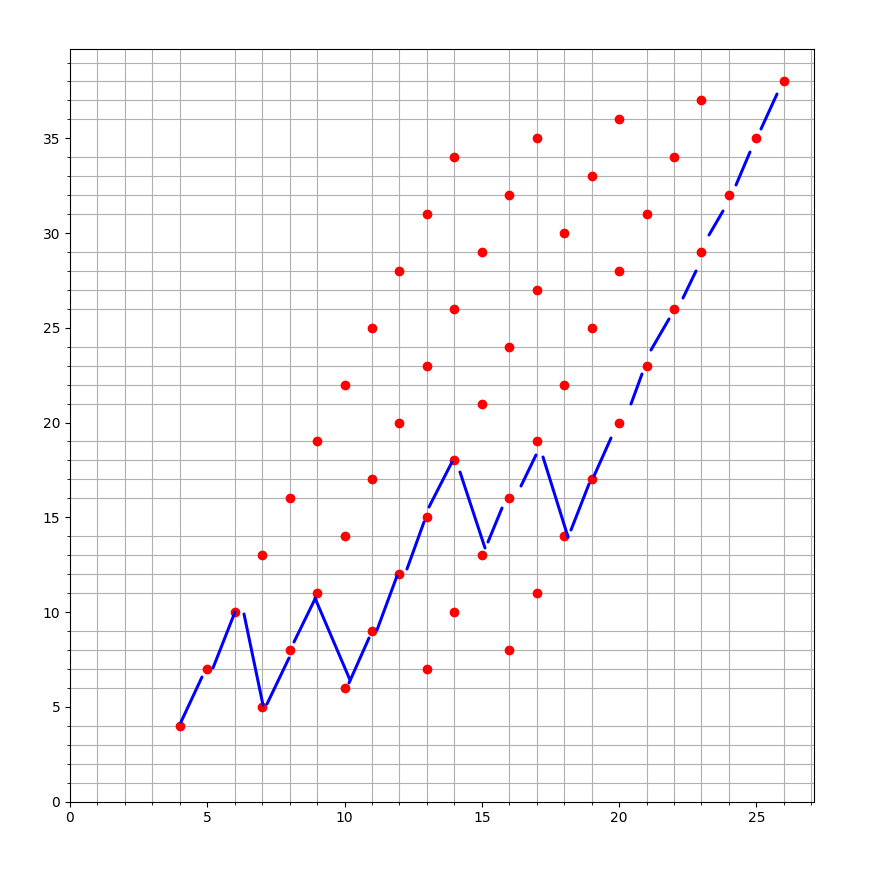
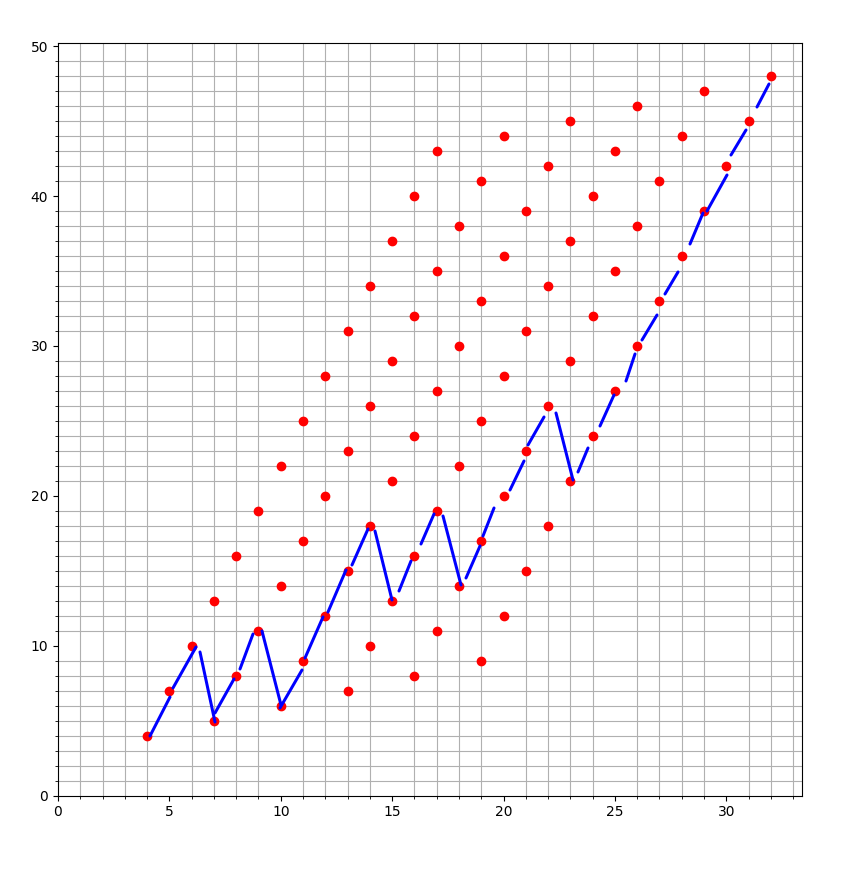
1到n的排列,进行k次冒泡排序(for i = 0..n-1{if a[i] > a[i+1]: swap(a[i],a[i+1])})以后
每一位与它前面的逆序对个数为v[i]
v[i] = count(a[j] > a[i] && j < i)
现在给定数组v,其中-1表示任意值, 求有多少个原始序列 能k次冒泡排序后,逆序对满足v
答案mod 998244353
保证-1<= vi <=i
范围
t <= 1000
k < n <= 1e6
2s
256MB
题解
观察冒泡排序过程中 逆对的变化
如果a[i]前面有比它大的, 那么一次冒泡排序后,至多有一个移动到它后面, 且a[i]移动到了a[i-1]
因此对于逆序对 v[0] v[1] v[2] ... v[n] 的变化是
如果v[i] > 0 , 那么一次排序后 v[i-1] = v[i]-1
对于v[i] == 0, 0 v[i+1] v[i+2] v[i+3] ... v[j-2] v[j-1] 0, 两个0之间其它非零
注意到上面 非0的结论, (v[i+1]-1) (v[i+2]-1) (v[i+3]-1) ... (v[j-2]-1) (v[j-1]-1) 0 (v[?j+1]-1),
即是这个0会移动到下一个0的前一个位置,a[j-1] = a[i]
所以0-index
最终v[i] == 0 操作前 v[i+k] <= k(反证法) , <= min(k,i)
最终v[i] > 0 操作前 v[i+k] = k
最终v[i] == -1 操作前 v[i+k] 任意(<=i)
最后k位一定是0
综上, 我们可以求得初始的v数组
其中 [0..k-1] 任意
其中 [k..n] 由按上述 平移确定具体情况
接下来讨论排列方案计算方式
如果完全自由就是n!,
考虑从后向前选, 如果位置i不受限制, 那么它有i+1种选法, 相当于每个位置的方案数和下标同增 w[i] = i+1(0-index)
如果它明确知道前面有几个比它小的, 那么只有唯一选法
如果它前面比它小的允许<=k, 那么它有k+1种选法, 相当于[0..k]每个一种
题目保证了v[i] 的范围,所以最多判断一下后k位是否为0即可
代码
https://codeforces.com/contest/1677/submission/156367090
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
| #include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define MOD 998244353
#define rep(i,a,n) for (ll i=a;i<(ll)n;i++)
#define per(i,a,n) for (ll i=n;i-->(ll)a;)
int n,k;
int v[1000010];
int main(){
int t;
cin>>t;
while(t--){
scanf("%d %d",&n,&k);
rep(i,0,n){
scanf("%d",v+i);
}
ll ans = 1;
rep(i,0,n){
if(i < k){
(ans*=i+1)%=MOD;
}else if(v[i-k] == -1){
(ans*=i+1)%=MOD;
}else if(v[i-k] == 0){
(ans*=k+1)%=MOD;
}
}
rep(i,0,k){
if(v[n-1-i] > 0)ans = 0;
}
printf("%lld\n",ans);
}
return 0;
}
|
总结
感觉还是考察 冒泡排序及其性质
参考
https://www.bilibili.com/video/BV1GS4y1b7SD
E
https://codeforces.com/contest/1677/problem/E
给定1到n的排列
q个询问
每次问[l..r] 中有多少子区间, 满足 子区间存在不同的两个数的乘积 等于 子区间最大值
范围
n <= 2e5
q <= 1e6
4s
1024MB
题解
a[1..n]为给的排列
离线, 把所有查询[l..r] 按r升序
for(i = 1..n) 在i == r 时,回答查询[l..r]
线段树, 叶子节点记录[l..j], (j<=r) 有多少个是满足的, 答案就是线段树的区间求和query(o,1,n,l,r)
问题: 遍历过程中i=>i+1时,也就是以i==r作为区间结束时,合法的区间起始l需要+1,但合法的l是散的,不是一个连续的区间, 这样更新复杂度高
考虑加入r时, 左侧比它大的端点的贡献, 首先用单调栈记录(坐标增加,值减少)
vector<pair<value,position>> stk, 其中(stk[i].value = a[stk[i].position])
那么加入{a[r],r} 后会移除值比它小的, 变成
stk[0] ... stk[i-1] stk[i] ... stk[j] {a[r],r}
讨论3部分贡献
以a[r] 为区间最大值, 那么必然 $(stk[j].position, r]$ 中找最右侧的位置k让a[k..r]中能有两个乘起来等于a[r], 这样, 就有$k-stk[j].position$ 个合法方案
以stk[i].value为区间最大值, 且stk[i].value 不是a[r]的倍数, $max(k) ,k \in (stk[i-1].position,stk[i].position]$, 贡献为$k-stk[i-1].position$, 因为不是倍数, 显然并不会因为多了a[r] 影响以这个值为最大值的左侧选取的$k$, 所以换个说法就是, 它以原来的贡献又贡献了一轮
以stk[i].value为区间最大值, 且stk[i].value 是a[r]的倍数, $max(k) ,k \in (stk[i-1].position,stk[i].position]$, 贡献为$k-stk[i-1].position$, 是倍数, 所以需要看stk[i].value/a[r]这个值所在的位置是否会更新k
这样去统计, 单调队列中
考虑变化
如果我们每个线段树节点记录了 (对右侧贡献的左端点数量x, 总贡献数c)
(x0,c0) => (x1,c1) 是怎么变化的呢
x1 = x0 + 那些a[r]倍数中超出来的长度
c1 = c0 + x1
注意的是, 可以lazytag记录有多少轮没有向下, 每次修改log级别个节点就行了
(这个方法感觉有实现问题, 我尝试做了一下,发现每次需要 c += x, 但是因为lazytag 的关系, 你一个节点上只能保存常数个x 和 常数个次数记录, 对于在 dep 层 的变化, lazytag down到dep+1层会覆盖x, 换句话说 lazy 的部分和历史每个节点内的x相关
官方的代码, 记录的是(x0,y0)
y0 = c0 - x0 * 轮次, y1 = c1 - x1*(轮次+1) = (x1+c0) - x1*(轮次+1) = y0 - (x1-x0) * 轮次
比记录和好的是,在不更新时(x,y)不会变,而c会变, 每次更新后所有节点都是正确的值, 因为lazy的部分只和当前轮次相关, 而这些轮次加和以后, 就是y的变化量
注意到 lazy的部分 (x1-x0) 要么是len要么是-len, 所以把符号给到轮次上, lazy轮次的和即可
而不是全覆盖的部分, 直接去更新到准确的(x,y)
代码
官方代码+注释
https://codeforces.com/contest/1677/submission/156392477
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
| #include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define rep(i,a,n) for (ll i=a;i<(ll)n;i++)
const int N=2e5;
#define SEG_ROOT 1,1,n
#define SEG_L (o<<1)
#define SEG_R (o<<1|1)
#define mid (l+r)/2
#define SEG_L_CHILD SEG_L,l,mid
#define SEG_R_CHILD SEG_R,mid+1,r
#define SEG_L_CHILD_Q SEG_L,l,mid,ql,qr
#define SEG_R_CHILD_Q SEG_R,mid+1,r,ql,qr
int n;
int a[N+10];
int a2i[N+10];
int di;
int d[N+10];
int i2di[N+10];
int ti;
int p[N+10];
ll ans[1000005];
vector<pair<int,int> >q[1000005];
vector<int> w[N + 10];
struct seg {
ll x;
ll y;
ll tg;
ll len;
} tr[N*4 + 10];
void make(int o,int l,int r){
tr[o].len=r-l+1;
if (l==r) return;
make(SEG_L_CHILD);
make(SEG_R_CHILD);
}
void down(int o) {
if (tr[o].x == tr[o].len) {
tr[SEG_L].x = tr[SEG_L].len;
tr[SEG_R].x = tr[SEG_R].len;
}
if (tr[o].x==0) {
tr[SEG_L].x=0;
tr[SEG_R].x=0;
}
if(tr[o].tg != 0){
assert(tr[o].x == tr[o].len || tr[o].x == 0);
tr[SEG_L].y+=tr[o].tg*tr[SEG_L].len;
tr[SEG_R].y+=tr[o].tg*tr[SEG_R].len;
tr[SEG_L].tg+=tr[o].tg;
tr[SEG_R].tg+=tr[o].tg;
tr[o].tg=0;
}
}
void up(int o) {
tr[o].x=tr[SEG_L].x+tr[SEG_R].x;
tr[o].y=tr[SEG_L].y+tr[SEG_R].y;
}
void clear(int o,int l,int r,int ql,int qr) {
if (ql <= l && r <= qr) {
assert(tr[o].x == tr[o].len);
tr[o].tg+=ti;
tr[o].y += ti*tr[o].len;
tr[o].x=0;
return;
}
down(o);
if (ql<=mid) clear(SEG_L_CHILD_Q);
if (qr>mid) clear(SEG_R_CHILD_Q);
up(o);
}
void add(int o,int l,int r,int ql,int qr) {
if (ql <= l && r <= qr) {
assert(tr[o].x == 0);
tr[o].tg += -ti;
tr[o].y += -ti*tr[o].len;
tr[o].x=tr[o].len;
return;
}
down(o);
if (ql<=mid) add(SEG_L_CHILD_Q);
if (qr>mid) add(SEG_R_CHILD_Q);
up(o);
}
ll find(int o,int l,int r,int ql,int qr) {
if (ql <= l && r <= qr) return tr[o].y+ti*tr[o].x;
down(o);
ll ret = 0;
if (ql<=mid) ret+=find(SEG_L_CHILD_Q);
if (qr>mid) ret+=find(SEG_R_CHILD_Q);
return ret;
}
int main() {
int m;
scanf("%d%d",&n,&m);
rep(i,1,n+1){
scanf("%d",&a[i]);
a2i[a[i]]=i;
}
rep(i,1,m+1) {
int l,r;
scanf("%d%d",&l,&r);
q[r].emplace_back(l,i);
}
rep(i,1,n+1)
for (int j=i;j<=n;j+=i)
w[j].emplace_back(i);
make(SEG_ROOT);
rep(i,1,n+1) {
while (di && a[d[di]]<a[i]) {
if (p[di]>d[di-1]) clear(SEG_ROOT,d[di-1]+1,p[di]);
i2di[d[di]]=0;
di--;
}
for (int j=a[i];j<=n;j+=a[i]) {
int k=i2di[a2i[j]];
if (!k) continue;
int l=d[k-1]+1,r=d[k];
int e=a2i[j/a[i]];
if (e<l || e>=i) continue;
e=min(e,r);
if (e<=p[k]) continue;
add(SEG_ROOT,p[k]+1,e);
p[k]=e;
}
d[++di]=i;
i2di[i]=di;
p[di]=d[di-1];
for (auto j:w[a[i]]) {
int l=d[di-1]+1;
int e1=a2i[j];
int e2=a2i[a[i]/j];
if (e2<=e1) continue;
if (e1<l || e2>i) continue;
if (e1<=p[di]) continue;
add(SEG_ROOT,p[di]+1,e1);
p[di]=e1;
}
ti++;
for (auto t:q[i]) ans[t.second] = find(SEG_ROOT,t.first,i);
}
rep(i,1,m+1) printf("%lld\n",ans[i]);
return 0;
}
|
总结
学会了一下新的线段树写法,以前我在左右拆点的时候, 会根据覆盖决定是
(ql,qr) => (ql,qr) 还是(ql,qr) => (ql,mid) 还是 (ql,qr) => (mid+1,qr) 终止条件是l == ql && r == qr
这里学到了把终止条件改成ql <= l && r <= qr, 这样的话, 传参就不用拆了(ql,qr) => (ql,qr)
参考
https://codeforces.com/contest/1678/attachments/download/16086/Codeforces%20Round%20789%20Editorial%20in%20Chinese.pdf
https://codeforces.com/blog/entry/102631
https://www.bilibili.com/video/BV1GS4y1b7SD